《2025年学习之友九年级数学上册北师大版》

4. 在平面直角坐标系内,一光源位于A(0,5)处,线段CD⊥x轴于D点,C坐标为(3,2),则CD在x轴上的影长为2,点C的影子的坐标为(5,0).

答案： 2;(5,0)

5. 如图,在圆桌的正上方有一盏吊灯.在灯光下,圆桌在地板上的投影是面积为$4πm^2$的圆.已知圆桌的高度为1.5m,圆桌面的半径为1m,则吊灯距圆桌面的高度是1.5 m.
]

答案： 1.5 m

6. 如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增加了3米,求小方行走的路程.
]

答案： 解:
∵AE⊥OD,GO⊥OD,
∴EA//GO,
∴△AEB∽△OGB,
∴$\frac{AE}{GO}=\frac{AB}{BO}$,
∴$\frac{1.6}{5.6}=\frac{AB}{AB+5}$,解得 AB=2 m;
∵OA 所在的直线行走到点 C 时,人影长度增加 3 米,
∴DC=5(m),
同理可得△DFC∽△DGO,
∴$\frac{FC}{GO}=\frac{CD}{DO}$,即$\frac{1.6}{5.6}=\frac{5}{5+5+AC}$,
解得 AC=7.5 m. 答:小方行走的路程 AC 为 7.5 m.

1. 一张圆形桌面的直径AB= 2米,高度为1.8米,桌面的上方有一盏电灯泡O.
(1)请在图中画出灯泡O发光时,桌面在地上的影子的最大宽度EF.
(2)若EF= 5米,请求出灯泡离地面的高度.
]

答案：
解:
(1)答案如图:

(2)连接 AB,作 OH⊥EF 于点 H,交 AB 于点 G,

∵AB//EF,
∴△OAB∽△OEF,
∴$\frac{AB}{EF}=\frac{OG}{OH}$,
即$\frac{2}{5}=\frac{OG}{OG+1.8}$,
解得 OG=1.2,
∴灯泡离地面的高度为 OH=OG+GH=1.2+1.8=3 米.

2. 如图,宁夏沙坡头盛典剧院舞台上的照明灯P射出的光线形成了圆锥体,∠APC是圆锥的高和底面直径AC所在的截面△PAC的顶角,即∠APC= 60°.已知舞台的形状ABCD是边长为6m的正方形,要使灯光恰好能照射到整个舞台,则照明灯P悬挂的高度是多少？

答案：
解:如图,连接 AC,PO,由题意可知点 O 在 AC 上,PO⊥AC.

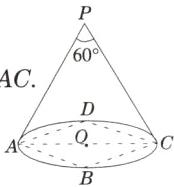
∵∠APC=60°,PA=PB,
∴PA=PC=AC,
∵四边形 ABCD 是边长为 6 m 的正方形,
∴AC=6$\sqrt{2}$ m,
∴OC=3$\sqrt{2}$ m,
∵PC=AC=6$\sqrt{2}$ m,
∴PO=3$\sqrt{6}$ m.