《2025年学习之友九年级数学上册北师大版》

3. 山顶有一铁塔 $ AB $ 的高度为 $ 20 $ 米,为测量山的高度 $ BC $,在山脚点 $ D $ 处测得塔顶 $ A $ 和塔基 $ B $ 的仰角分别为 $ 60° $ 和 $ 45° $,求山的高度 $ BC $.(结果保留根号)
]

答案： 解:
∵ ∠CDB=45°,
∴ ∠DBC=45°,
∴ BC=CD.在Rt△ACD中,tan 60°=AC/CD,
∴ AC=tan 60°×CD,即20 + CD=tan 60° CD,
∴ CD=10(√3 +1)米,
∴ BC=10(√3 +1)米.

4. 某风景区内有一古塔 $ AB $,在塔的一侧有一建筑物,当光线与水平面的夹角是 $ 30° $ 时,塔在建筑物的墙上留下了高为 $ 3 $ 米的影子 $ CD $；而当光线与地面的夹角是 $ 45° $ 时,塔尖 $ A $ 在地面上的影子 $ E $ 与建筑物的距离 $ EC $ 为 $ 15 $ 米($ B $,$ E $,$ C $ 在一条直线上),求塔 $ AB $ 的高度.(结果保留根号)
]

答案： 解:过D作DF⊥AB于点F,
∵ ∠BEA=∠BAE=45°,
∴ BA=BE.在Rt△AFD中,tan 30°=AF/DF,
∴ AF=tan 30° DF,
∴ BE - 3=tan 30°×(BE + 15),
∴ BE - 3=√3/3 BE + 5√3,
∴ AB=BE=(12 + 9√3)米.

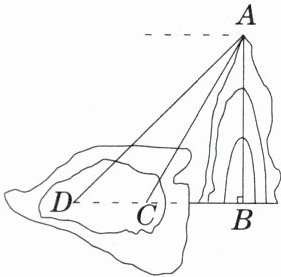
1. 某人要在公园的小山 $ AB $ 上测量湖中两个小岛 $ C $,$ D $ 间的距离.从山顶 $ A $ 处测得湖中小岛 $ C $ 的俯角为 $ 60° $,测得湖中小岛 $ D $ 的俯角为 $ 45° $.已知小山 $ AB $ 的高为 $ 180 $ 米,求小岛 $ C $,$ D $ 间的距离.(结果不取近似值)
]

答案： 解:在Rt△ABC中,tan 60°=AB/BC,
∴ BC=AB/tan 60°=180/√3=60√3(米).在Rt△ABD中,AB=BD=180米,
∴ CD=BD - BC=(180 - 60√3)米.

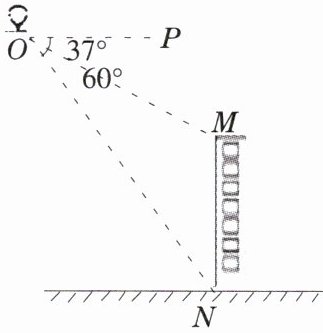
2. 如图,某研究所利用热气球 $ O $ 测量某居民楼 $ MN $ 的高度.从热气球处测得大楼顶部 $ M $ 的俯角为 $ 37° $,大楼底部 $ N $ 的俯角为 $ 60° $,此时热气球 $ O $ 离地面的高度为 $ 120 $ m.试求大楼 $ MN $ 的高度.(结果精确到 $ 0.1 $ m,参考数据：$ \sin 37° \approx 0.60 $,$ \cos 37° \approx 0.80 $,$ \tan 37° \approx 0.75 $,$ \sqrt{2} \approx 1.41 $,$ \sqrt{3} \approx 1.73 $)
]

答案： 解:过O作OH⊥MN,垂足为H,由已知∠HON=60°,∠HOM=37°,由题意可知:NH=120 m.在Rt△HON中,由tan∠HON=HN/OH,即tan60°=120/OH,得OH=120/√3=40√3.在Rt△HOM中,由tan∠HOM=HM/OH,即tan37°=HM/(40√3),得HM=40√3×0.75≈51.9.因此MN=HN - HM=120 - 51.9=68.1.即大楼MN的高度约为68.1m.