《2025年学习之友九年级数学上册北师大版》

2. 一斜坡长 $70$ m,它的高为 $5$ m,将重物从斜坡起点推到坡上 $20$ m 处停下,停下地点的高度为(C)。
A.$\frac{11}{7}$ m
B.$\frac{9}{7}$ m
C.$\frac{10}{7}$ m
D.$\frac{3}{2}$ m

答案： C

3. 小芳在打网球时,她击球的高度是 $2.4$ m,为使球恰好能过网(网高 $0.8$ m),且落在对方区域离网 $5$ m 的位置上(如图),则她应站在离网(B)。
A.$15$ m 处
B.$10$ m 处
C.$8$ m 处
D.$75$ m 处

答案： B

4. 高为 $3$ m 的木条,在地面上的影长为 $12$ m,这时,测得一建筑物的影长为 $36$ m,则该建筑物的高度是9m。

答案： 9m

5. 一油桶高 $0.8$ m,桶内有油,一根木棒长 $1$ m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长 $0.8$ m,则桶内油面的高度为0.64m。

答案： 0.64

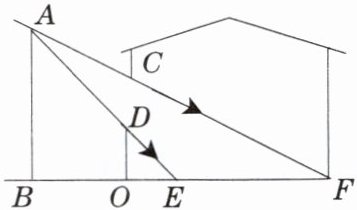
6. 如图,小明家窗外有一堵围墙 $AB$,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点 $C$ 射进房间的地板 $F$ 处,中午太阳光恰好能从窗户的最低点 $D$ 射进房间的地板 $E$ 处,小明测得窗户距地面的高度 $OD = 1$ m,窗高 $CD = 1.5$ m,并测得 $OE = 1$ m,$OF = 5$ m,求围墙 $AB$ 的高度。

答案： 解:延长OD，$\because DO⊥BF$，
$\therefore ∠DOE = 90^{\circ}$，$\because OD = 1m$，
$OE = 1m$，$\therefore ∠DEB = 45^{\circ}$.
$\because AB⊥BF$，$\therefore ∠BAE = 45^{\circ}$，
$\therefore AB = BE$.
设$AB = EB = xm$，
$\because AB⊥BF$，$CO⊥BF$，$\therefore AB// CO$，
$\therefore \triangle ABF\backsim \triangle COF$，$\therefore \frac{AB}{BF}=\frac{CO}{OF}$，
$\therefore \frac{x}{4 + x}=\frac{1.5 + 1}{5}$.
解得$x = 4$.
经检验：$x = 4$是原方程的解.
答:围墙AB的高度是4m.

7. 如图,某同学要测量某烟囱的高度,他将一面镜子放在地面上的某一位置,然后站到与镜子、烟囱成一条直线的地方,刚好从镜中看到烟囱的顶部,如果这名同学身高为 $1.65$ m,他到镜子的距离是 $2$ m,测得镜面到烟囱的距离为 $20$ m,求烟囱的高度。

答案：
解:过点C作镜面的法线FC，由光学原理得$∠ECF = ∠ACF$.

$\because ∠ACB = 90^{\circ}-∠FCA$，$∠ECD = 90^{\circ}-∠FCE$，
$\therefore ∠ACB = ∠ECD$，
又$\because ∠EDC = ∠ABC = 90^{\circ}$，
$\therefore \triangle ABC\backsim \triangle EDC$，
$\therefore \frac{AB}{BC}=\frac{ED}{DC}$，即$\frac{1.65}{2}=\frac{ED}{20}$，解得$ED = 16.5m$.
答:烟囱的高度为16.5米.

一天,数学课外活动小组的同学们带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度,来评估这些坑道对河道的影响,如图是同学们选择(确保测量过程中无安全隐患)的测量对象,测量方案如下：
①先测出沙坑坑沿的圆周长是 $34.54$ m；
②甲同学直立于沙坑坑沿的圆周所在的平面上,经过适当调整自己所处的位置,当他位于 $B$ 时他的视线恰好经过沙坑坑沿圆周上一点 $A$ 看到坑底 $S$(甲同学的视线起点 $C$ 与点 $A$,点 $S$ 三点共线),经测量：$AB = 1.2$ m,$BC = 1.6$ m。
根据以上测量数据,求“圆锥形坑”的深度(圆锥的高)。($\pi$ 取 $3.14$,结果精确到 $0.1$ m)

答案：
解:取圆锥底面圆心O，连接OS、OA，则$∠O = ∠ABC = 90^{\circ}$，$OS// BC$，
$\therefore ∠ACB = ∠ASO$，
$\therefore \triangle SOA\backsim \triangle CBA$，

$\therefore \frac{OS}{BC}=\frac{OA}{BA}$，
$\because OA=\frac{34.54}{2\pi}\approx 5.5$米，$BC = 1.6$米，$AB = 1.2$米，
$\therefore OS=\frac{5.5×1.6}{1.2}\approx 7.3m$.
答:“圆锥形坑”的深度约为7.3米.