《2025年学习之友九年级数学上册北师大版》

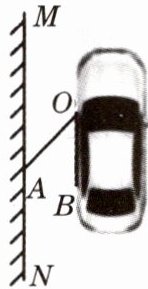
6. 如图,一辆小汽车停在离墙约$0.7$米的地方,车身与墙平行,当司机将车门$OB打开角度\angle AOB为40^{\circ}$时,车门刚好碰到墙,求车门的宽度？(结果精确到$0.1$米,参考数据：$\sin 40^{\circ}\approx0.64$,$\cos 40^{\circ}\approx0.77$,$\tan 40^{\circ}\approx0.84$)

答案： 解:如图,过点A作AC⊥OB,垂足为C.在Rt△AOC中,
∵∠AOC = 40°,AC = 0.7米,sin∠AOC = $\frac{AC}{OA}$
∴OB = OA = $\frac{AC}{sin∠AOC}$≈$\frac{0.7}{0.64}$≈1.1(米)
∴车门宽约1.1米

1. 斜坡$AC$的坡度(坡比)为$1:\sqrt{3}$,$AC = 10$米。坡顶有一旗杆$BC$,旗杆顶端$B点与A点有一条彩带AB$相连,$AB = 14$米。试求旗杆$BC$的高度。

答案： 解:如图,延长BC交AD于E点，则CE⊥AD.在Rt△ACE中,AC = 10,由坡比为1:$\sqrt{3}$可知:∠CAE = 30°,
∴CE = AC·sin30° = 10×$\frac{1}{2}$ = 5,AE = AC·cos30° = 10×$\frac{\sqrt{3}}{2}$ = 5$\sqrt{3}$.在Rt△ABE中,BE = $\sqrt{AB^2 - AE^2}$ = $\sqrt{14^2 - (5\sqrt{3})^2}$ = 11.
∵BE = BC + CE,
∴BC = BE - CE = 11 - 5 = 6 (米).故旗杆的高度为6米.

2. 如图,一艘海轮位于灯塔$P的北偏西53^{\circ}$方向,距离灯塔$100海里的A$处,它沿正南方向航行一段时间后,到达位于灯塔$P的西南方向的B$处。
(1)求出$B处到灯塔P$的距离；
(2)求$AB$的距离。
(结果取整数,参考数据：$\sin 53^{\circ}\approx0.80$,$\cos 53^{\circ}\approx0.60$,$\tan 53^{\circ}\approx1.33$,$\sqrt{2}\approx1.41$)

答案：
(1)由题意可知:∠A = 53°,∠B = 45°,PA = 100.在Rt△ACP中sinA = $\frac{PC}{PA}$
∴PC = PA·sin53°≈100×0.8 = 80(海里)
∵∠BPC = 45°,AB⊥PC,
∴∠PBC = ∠BPC = 45°,
∴BC = PC≈80海里,
∴BP = $\sqrt{PC^2 + BC^2}$ = $\sqrt{80^2 + 80^2}$≈113
∴B处到灯塔P的距离约为113海里.
(2)
∵在Rt△ACP中cosA = $\frac{AC}{AP}$
∴AC = AP·cos53°≈100×0.60 = 60(海里)
∴AB = AC + BC = 60 + 80 = 140(海里)
∴AB的距离约为140海里。

3. 某村决定将河边一台阶进行改造。在如图的台阶横断面中,将坡面$AB的坡角由45^{\circ}减至30^{\circ}$。已知原坡面的长为$6m$($BC$所在地面为水平面)。
(1)改造后的台阶坡面会缩短多少？
(2)改造后的台阶高度会降低多少？
(结果精确到$0.1m$,$\sqrt{2}\approx1.41$,$\sqrt{3}\approx1.73$)

答案：
(1)在Rt△ABC中,AB = 6,
∴BC = 6sin 45° = 3$\sqrt{2}$在Rt△BCD中,BD = $\frac{BC}{cos30°}$ = 2$\sqrt{6}$,
∴AB - BD = 6 - 2$\sqrt{6}$≈1.1214≈1.1(m),即台阶坡面会缩短1.1m.
(2)AC = BC = 3$\sqrt{2}$,CD = BD·sin30° = $\sqrt{6}$,
∴AD = AC - CD = 3$\sqrt{2}$ - $\sqrt{6}$≈1.7907≈1.8(m),即台阶高度会降低1.8m.