《2025年学习之友九年级数学上册北师大版》

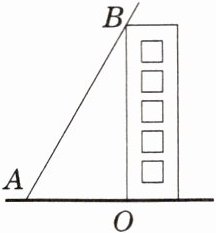
1. 为测量一幢大楼的高度,在地面上距离楼底 $ O $ 点 $ 20 $ m 的点 $ A $ 处,测得楼顶 $ B $ 点的仰角 $ \angle OAB = 60° $,则这幢大楼的高度为(D)m.

A.$ 40\sqrt{3} $
B.$ 10\sqrt{3} $
C.$ 2\sqrt{3} $
D.$ 20\sqrt{3} $
]

答案： D

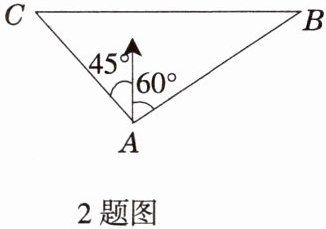
2. 如图,一艘轮船在小岛 $ A $ 的西北方向距小岛 $ 40 $ 海里的 $ C $ 处,沿正东方向航行一段时间后到达小岛 $ A $ 的北偏东 $ 60° $ 的 $ B $ 处,则该船行驶的路程为 20√2 + 20√6海里.
]

答案： 20√2 + 20√6

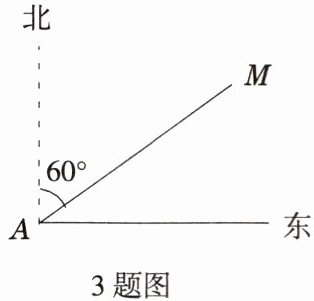
3. 如图,某渔船在海面上朝正东方向匀速航行,在 $ A $ 处观测到灯塔 $ M $ 在北偏东 $ 60° $ 方向上,且 $ AM = 150 $ 海里.那么该船继续航行75√3海里,可使渔船到达离灯塔 $ M $ 距离最近的位置.

答案： 75√3

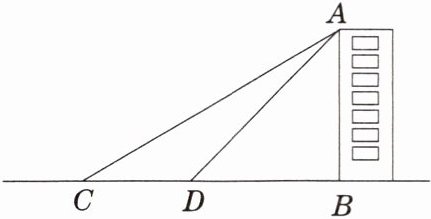
4. 九年级学生要测量学校一幢教学楼的高度.他们先在点 $ C $ 测得教学楼 $ AB $ 的顶点 $ A $ 的仰角为 $ 30° $,然后向教学楼前进 $ 60 $ 米到达点 $ D $,又测得点 $ A $ 的仰角为 $ 45° $.请你根据这些数据,求出这幢教学楼的高度.(计算过程和结果均不取近似值)
]

答案： 解:由已知,可得∠ACB=30°,∠ADB=45°,
∴ 在Rt△ADB中,BD=AB.又在Rt△ABC中,
∵ tan 30°=AB/BC,
∴ AB/BC=√3/3,即BC=√3 AB.
∵ BC=CD+BD,
∴ √3 AB=CD+AB,即(√3 -1)AB=60.
∴ AB=60/(√3 -1)=30(√3 +1)(米).故教学楼的高度为30(√3 +1)米.

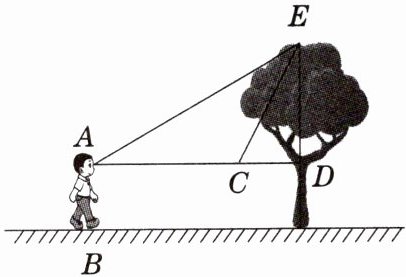
1. 某人想测量一棵大树的高度. 他站在 $ B $ 处仰望树顶,测得仰角为 $ 30° $,再往大树的方向前进 $ 4 $ m,到达 $ C $ 处,测得仰角为 $ 60° $,已知此人身高($ AB $)为 $ 1.6 $ m,则这棵树的高度为 5.1 米.(结果精确到 $ 0.1 $ m,$ \sqrt{3} \approx 1.73 $)
]

答案： 5.1

2. 某校校庆,要从楼顶 $ A $ 处向地面拉几条彩带. 工作人员在 $ C $ 处测得 $ \angle ACB = 60° $,在 $ D $ 处测得 $ \angle ADB = 30° $,$ B $,$ C $,$ D $ 在同一水平直线上,$ CD = 12 $ 米.问：彩带 $ AD $ 的长应为多少米？(结果保留根号)

答案： 解:根据题意得:∠ABC=90°,
∵ ∠ACB=60°,∠ADB=30°,
∴ ∠CAD=∠ACB - ∠ADB=30°,
∴ ∠CAD=∠ADB,
∴ AC=CD=12米,在Rt△ABC中,AB=AC·sin 60°=12×√3/2=6√3(米),BC=AC·cos 60°=12×1/2=6(米),
∴ BD=BC + CD=6 + 12=18(米),在Rt△ABD中,AD=√(AB² + BD²)=12√3(米).故彩带AD的长应为12√3米.