第112页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
1. 用计算器计算$\tan 46^{\circ}$(精确到$0.01$)等于(
A.$1.03$
B.$1.04$
C.$1.05$
D.$1.06$
B
)。A.$1.03$
B.$1.04$
C.$1.05$
D.$1.06$
答案:
B
2. 若用数学课本上使用的科学计算器计算$\sin 42^{\circ}16'$,按键顺序正确的是(
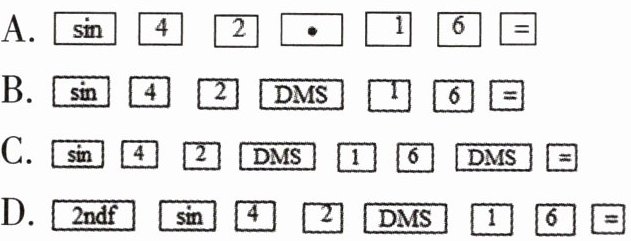
A.$\boxed{\sin}\ \boxed{4}\ \boxed{2}\ \boxed{\cdot}\ \boxed{1}\ \boxed{6}\ \boxed{=}$
B.$\boxed{\sin}\ \boxed{4}\ \boxed{2}\ \boxed{DMS}\ \boxed{1}\ \boxed{6}\ \boxed{=}$
C.$\boxed{\sin}\ \boxed{4}\ \boxed{2}\ \boxed{DMS}\ \boxed{1}\ \boxed{6}\ \boxed{DMS}\ \boxed{=}$
D.$\boxed{2ndf}\ \boxed{\sin}\ \boxed{4}\ \boxed{2}\ \boxed{DMS}\ \boxed{1}\ \boxed{6}\ \boxed{=}$
C
)。
A.$\boxed{\sin}\ \boxed{4}\ \boxed{2}\ \boxed{\cdot}\ \boxed{1}\ \boxed{6}\ \boxed{=}$
B.$\boxed{\sin}\ \boxed{4}\ \boxed{2}\ \boxed{DMS}\ \boxed{1}\ \boxed{6}\ \boxed{=}$
C.$\boxed{\sin}\ \boxed{4}\ \boxed{2}\ \boxed{DMS}\ \boxed{1}\ \boxed{6}\ \boxed{DMS}\ \boxed{=}$
D.$\boxed{2ndf}\ \boxed{\sin}\ \boxed{4}\ \boxed{2}\ \boxed{DMS}\ \boxed{1}\ \boxed{6}\ \boxed{=}$
答案:
C
3. 若角$\alpha,\beta$都是锐角,以下结论:
①若$\alpha<\beta$,则$\sin\alpha<\sin\beta$;
②若$\alpha<\beta$,则$\cos\alpha<\cos\beta$;
③若$\alpha<\beta$,则$\tan\alpha<\tan\beta$;
④若$\alpha+\beta=90$,则$\sin\alpha=\cos\beta$。
其中正确的是(
A.①②
B.①②③
C.①③④
D.①②③④
①若$\alpha<\beta$,则$\sin\alpha<\sin\beta$;
②若$\alpha<\beta$,则$\cos\alpha<\cos\beta$;
③若$\alpha<\beta$,则$\tan\alpha<\tan\beta$;
④若$\alpha+\beta=90$,则$\sin\alpha=\cos\beta$。
其中正确的是(
C
)。A.①②
B.①②③
C.①③④
D.①②③④
答案:
C
4. 利用计算器计算(精确到$0.0001$)。
(1)$\sin 56^{\circ}12'=$
(2)$\cos 67^{\circ}15'30''=$
(3)$\tan 88^{\circ}56'55''=$
(4)$\tan 25^{\circ}+\tan 65^{\circ}=$
(1)$\sin 56^{\circ}12'=$
0.8310
;(2)$\cos 67^{\circ}15'30''=$
0.3866
;(3)$\tan 88^{\circ}56'55''=$
54.4892
;(4)$\tan 25^{\circ}+\tan 65^{\circ}=$
2.6108
。
答案:
(1)0.8310
(2)0.3866
(3)54.4892
(4)2.6108
(1)0.8310
(2)0.3866
(3)54.4892
(4)2.6108
5. 根据下列条件求出$\angle A$的度数。
(1)$\sin A = 0.37$;
(2)$\cos A = 0.63$;
(3)$\tan A = 3.465$。
(1)$\sin A = 0.37$;
(2)$\cos A = 0.63$;
(3)$\tan A = 3.465$。
答案:
(1)∠A = 21°48′
(2)∠A = 50°57'
(3)∠A = 73°54'7''
(1)∠A = 21°48′
(2)∠A = 50°57'
(3)∠A = 73°54'7''
1. 下列各式正确的是(
A.$\tan 70^{\circ}×\tan 20^{\circ}=1$
B.$\cos 35^{\circ}+\cos 35^{\circ}=\cos 70^{\circ}$
C.$\sin 40^{\circ}=2\sin 20^{\circ}$
D.$\tan 15^{\circ}>\tan 20^{\circ}$
A
)。A.$\tan 70^{\circ}×\tan 20^{\circ}=1$
B.$\cos 35^{\circ}+\cos 35^{\circ}=\cos 70^{\circ}$
C.$\sin 40^{\circ}=2\sin 20^{\circ}$
D.$\tan 15^{\circ}>\tan 20^{\circ}$
答案:
A
2. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle A = 30^{\circ}$,$AC = 2$,则$S_{\triangle ABC}$等于(
A.$\frac{4}{3}$
B.$3$
C.$\frac{3\sqrt{3}}{2}$
D.$\frac{2\sqrt{3}}{3}$
D
)。A.$\frac{4}{3}$
B.$3$
C.$\frac{3\sqrt{3}}{2}$
D.$\frac{2\sqrt{3}}{3}$
答案:
D
3. 比较大小:
(1)$\cos 35^{\circ}$
(2)若$\sin\alpha = 0.3276$,$\sin\beta = 0.3274$,则
(1)$\cos 35^{\circ}$
>
$\cos 45^{\circ}$,$\tan 50^{\circ}$<
$\tan 60^{\circ}$;(2)若$\sin\alpha = 0.3276$,$\sin\beta = 0.3274$,则
α>β
。
答案:
(1)>;<
(2)α>β
(1)>;<
(2)α>β
4. 小明发现在教学楼走廊上有一拖把以$15^{\circ}$的倾斜角斜靠在栏杆上,严重影响了同学们的行走安全。他自觉地将拖把挪动位置,使其倾斜角为$75^{\circ}$,如果拖把的总长为$1.80m$,则小明拓宽了行路通道
1.27
m。(结果精确到$0.01m$)
答案:
1.27
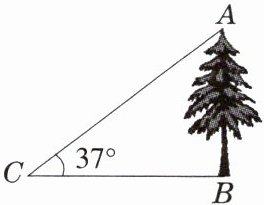
5. 如图,在一次数学课外实践活动中,小文在点$C处测得树的顶端A的仰角为37^{\circ}$,$BC为20m$,求树高$AB$。(参考数据:$\sin 37^{\circ}\approx0.60$,$\cos 37^{\circ}\approx0.80$,$\tan 37^{\circ}\approx0.75$)

答案:
解:根据题意得:AB⊥BC,∠C = 37°在Rt△ABC中,tanC = $\frac{AB}{BC}$
∴AB = BCtan37°≈20×0.75 = 15
∴树高约为15米。
∴AB = BCtan37°≈20×0.75 = 15
∴树高约为15米。
查看更多完整答案,请扫码查看


