《2025年学习之友九年级数学上册北师大版》

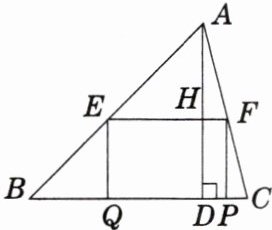
6. 如图,在 $ \triangle ABC $ 中,$ \angle B = 45° $,$ BC = 5 $,高 $ AD = 4 $,矩形 $ EFPQ $ 的一边 $ QP $ 在 $ BC $ 边上,点 $ E $,$ F $ 分别在 $ AB $,$ AC $ 上,$ AD $ 交 $ EF $ 于点 $ H $. 设 $ EF = x $,则当 $ x $ 为何值时,矩形 $ EFPQ $ 的面积最大？请求出其最大面积.

答案： 解:在矩形$EFPQ$中,$EF// PQ$,$\therefore \angle AEF=\angle B$,$\angle AFE=\angle C$,$\therefore \triangle AEF\backsim\triangle ABC$.$\because AD\perp BC$,$EF// PQ$,$\therefore AH\perp EF$,$\therefore \frac{AH}{AD}=\frac{EF}{BC}$.设矩形$EFPQ$的面积为$y$.$\because \frac{AH}{AD}=\frac{EF}{BC}$,$\therefore \frac{AH}{4}=\frac{x}{5}$,$\therefore AH=\frac{4}{5}x$,$\therefore DH=4-\frac{4}{5}x$,$\therefore y=-\frac{4}{5}x^2+4x=-\frac{4}{5}(x-\frac{5}{2})^2+5(0＜x＜5)$.又$\because a=-\frac{4}{5}＜0$,$\therefore$ 当$x=\frac{5}{2}$时,$y$有最大值$5$.即当$x=\frac{5}{2}$时,矩形$EFPQ$的面积最大,最大面积为$5$.

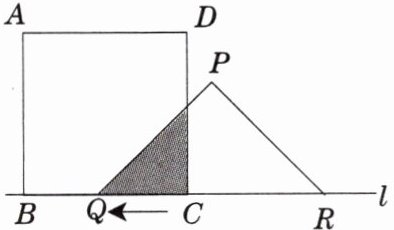
有一边长为 $ 5 \, cm $ 的正方形 $ ABCD $ 和等腰 $ \triangle PQR $,$ PQ = PR = 5 \, cm $,$ QR = 8 \, cm $,点 $ B $,$ C $,$ Q $,$ R $ 在同一条直线 $ l $ 上,当 $ C $,$ Q $ 两点重合时,等腰 $ \triangle PQR $ 以 $ 1 \, cm/秒 $ 的速度沿直线 $ l $ 按箭头所示方向开始匀速运动,$ t $ 秒后正方形 $ ABCD $ 与等腰 $ \triangle PQR $ 重合部分的面积为 $ S \, cm^2 $.
解答下列问题：
当 $ t = 3 $ 时,求 $ S $ 的值；
当 $ t = 5 $ 时,求 $ S $ 的值；
当 $ 5 \leq t \leq 8 $ 时,求 $ S $ 与 $ t $ 的函数关系式,并求出 $ S $ 的最大值.

答案：
解:
(1)如图,作$PE\perp QR$,$E$为垂足.$\because PQ=PR$,$\therefore QE=RE=\frac{1}{2}QR=4$,在$Rt\triangle PEQ$中,$PE=\sqrt{5^2-4^2}=3$;当$t=3$时,$QC=3$,设$PQ$与$DC$交于点$G$.$\because PE// DC$,$\therefore \triangle QCG\backsim\triangle QEP$.$\frac{S}{S_{\triangle QEP}}=(\frac{3}{4})^2$$\because S_{\triangle QEP}=\frac{1}{2}×4×3=6$,$\therefore S=(\frac{3}{4})^2×6=\frac{27}{8}(cm^2)$.
(2)当$t=5$时,$CR=3$.如图2,设$PR$与$DC$交于$G$,由$\triangle RCG\backsim\triangle REP$,可求出$CG=\frac{9}{4}$,所以,$S_{\triangle RCG}=\frac{1}{2}×3×\frac{9}{4}=\frac{27}{8}(cm^2)$,$S=12-\frac{27}{8}=\frac{69}{8}(cm^2)$.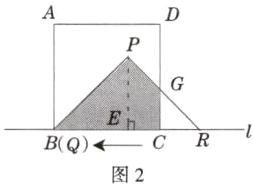
(3)当$5\leqslant t\leqslant8$时,$QB=t-5$,$RC=8-t$,设$PQ$交$AB$于点$H$,$PR$交$CD$于点$G$,如图3,$\because \triangle QBH\backsim\triangle QEP$,$EQ=4$,$BQ:EQ=(t-5):4$,$\therefore S_{\triangle BQH}:S_{\triangle PEQ}=(t-5)^2:4^2$,又$S_{\triangle PEQ}=6$,$\therefore S_{\triangle BQH}=\frac{3}{8}(t-5)^2$.由$\triangle RCG\backsim\triangle REP$,同理得$S_{\triangle RCG}=\frac{3}{8}(8-t)^2$,$\therefore S=12-\frac{3}{8}(t-5)^2-\frac{3}{8}(8-t)^2$,即$S=-\frac{3}{4}t^2+\frac{39}{4}t-\frac{171}{8}$.当$t=-\frac{\frac{39}{4}}{2×(-\frac{3}{4})}=\frac{13}{2}$时,$S$最大,$S$的最大值为$\frac{165}{16}(cm^2)$.