《2025年学习之友九年级数学上册北师大版》

1. 下列函数解析式中,一定为二次函数的是(C)。
A.$ y = 3x - 1 $
B.$ y = ax^{2} + bx + c $
C.$ s = 2t^{2} - 2t + 1 $
D.$ y = x^{2} + \frac{1}{x} $

答案： C

2. 已知二次函数 $ y = 1 + 5x^{2} - 3x $,则二次项系数 $ a = $5,一次项系数 $ b = $-3,常数项 $ c = $1。

答案： 5;-3;1

3. 函数 $ y = (m + 2)x^{m^{2} - 2} + 2x - 1 $ 是二次函数,则 $ m = $2。

答案： 2

4. 半径为 3 的圆,如果半径增加 $ 2x $,则面积 $ S $ 与 $ x $ 之间的函数表达式为(D)。
A.$ S = 2\pi(x + 3)^{2} $
B.$ S = 4\pi x^{2} + 12x + 9 $
C.$ S = 9\pi + x $
D.$ S = 4\pi x^{2} + 12\pi x + 9\pi $

答案： D

5. 某商店从厂家以每件 21 元购进一批商品,若每件商品定价 $ x $ 元,则可卖出 $ (350 - 10x) $ 件。(1)写出该商店出售此商品的利润 $ y $(元) 与商品 $ x $(元) 的函数关系式；(2)当售价定为多少元时,可获利 450 元？

答案：
(1)$y=(x - 21)(350 - 10x)= - 10x^{2}+560x - 7350$
(2)当$y = 450$时,即$- 10x^{2}+560x - 7350 = 450$，解得$x_{1}=30$，$x_{2}=26$
所以当售价定为26元或30元时，可获利450元

1. 函数：① $ y = \sqrt{3}x^{2} - 2 $；② $ y = x^{2} - x(1 + x) $；③ $ y = x^{2}(x^{2} - 1) + 2 $；④ $ y = x^{\frac{1}{2}} + x $；⑤ $ y = x(1 - x) $。其中二次函数的个数为(B)。
A.1
B.2
C.3
D.4

答案： B

2. 已知函数 $ y = (m - 1)x^{m^{2} - 5m + 7} + (m - 3)(m + 1) $,(1)当 $ m $ 为2或3时是一次函数；(2)当 $ m $ 为3时是正比例函数；(3)当 $ m $ 为$\frac{5 + \sqrt{5}}{2}$或$\frac{5 - \sqrt{5}}{2}$时是二次函数。

答案：
(1)2或3　
(2)3
(3)$\frac{5 + \sqrt{5}}{2}$或$\frac{5 - \sqrt{5}}{2}$

3. 若函数 $ y = (m - 2)x^{m^{2} + m - 4} + (m + 3)x + 2 $ 是二次函数,求 $ m $ 的值,并求出这个函数。

答案： 解:由题意得:$m^{2}+m - 4 = 2$，解得$m_{1}=-3$，$m_{2}=2$。
又$\because m - 2 \neq 0$，$\therefore m \neq 2$，$\therefore m = - 3$，$y = - 5x^{2}+2$。

4. 下图为一相框,若内部的相片尺寸是 $ 3×4 $,为了美观外部用宽为 $ x $ 的彩纸装裱。若装裱部分面积为 $ y $,试猜想 $ y $ 是 $ x $ 的什么函数,并说明理由。

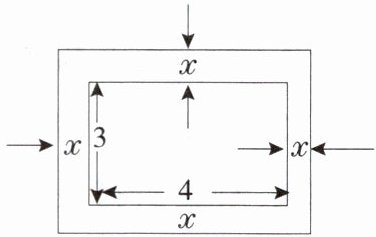
答案： 解:由题意得:
$y=(4 + 2x)(3 + 2x)-4×3$
$=4x^{2}+14x$
$y$是$x$的二次函数。

5. 如图是一个用 18 米的篱笆围成的两个矩形鸡舍,若公共边 $ EF $ 的长为 $ x $,矩形 $ ABCD $ 的面积为 $ y $,求出 $ y $ 与 $ x $ 之间的函数关系式,并求出自变量 $ x $ 的取值范围。

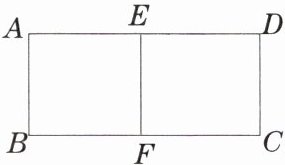
答案： 解:由题意得:
$y=(\frac{18 - 3x}{2})\cdot x=-\frac{3}{2}x^{2}+9x$，
$0＜x＜6$。

如图,校园要建苗圃,其形状为直角梯形,有两边借用夹角为 $ 135^{\circ} $ 的两面墙,另外两边是总长为 30 m 的铁栅栏。(1)写出梯形的面积 $ y $($ m^{2} $)与高 $ x $($ m $)的表达式；(2)求 $ x $ 的取值范围。

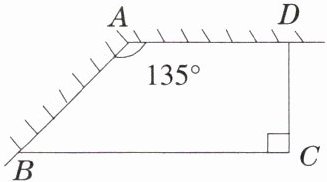
答案： 解:如图，过点A作$AE⊥BC$于点E，连接DE，则四边形ADCE为矩形，$DC = AE = xm$，
$∠DAE = ∠AEB = 90^{\circ}$，
则$∠BAE = ∠BAD - ∠EAD = 45^{\circ}$。
在$Rt\triangle ABE$中，
$\because ∠AEB = 90^{\circ}$，$∠BAE = 45^{\circ}$，
$\therefore DC = AE = BE = xm$，
$\therefore AD = CE = (30 - 2x)m$，
$\therefore$梯形$ABCD$的面积$y=\frac{1}{2}(AD + BC)\cdot CD=\frac{1}{2}(30 - 2x + 30 - x)\cdot x=-\frac{3}{2}x^{2}+30x$；
(2)由题意可知$\begin{cases}x＞0\\30 - 2x＞0\end{cases}$
$\therefore 0＜x＜15$。