《2025年学习之友九年级数学上册北师大版》

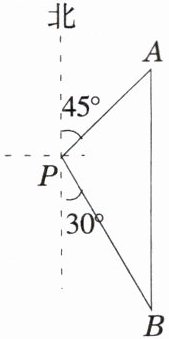
6. 如图,一艘海轮位于灯塔 $ P $ 的东北方向,距离灯塔 80 海里的 $ A $ 处,它沿正南方向航行一段时间后,到达位于灯塔 $ P $ 的南偏东 $ 30^{\circ} $ 方向上的 $ B $ 处。
(1) 求海轮从 $ A $ 处到 $ B $ 处的途中与灯塔 $ P $ 之间的最短距离(结果保留根号)；
(2) 若海轮以每小时 30 海里的速度从 $ A $ 处到 $ B $ 处,试判断海轮能否在 5 小时内到达 $ B $ 处,并说明理由。
(参考数据：$ \sqrt{2}\approx1.41 $,$ \sqrt{3}\approx1.73 $,$ \sqrt{6}\approx2.45 $)

答案： 解:
(1)作PC⊥AB于C,如图所示:
则∠PCA=∠PCB=90°,
由题意得:PA=80,∠APC=45°,∠BPC=90°-30°=60°,
∴△APC是等腰直角三角形,∠B=30°,
∴AC=PC=√2/2PA=40√2(海里).
答:海轮从A处到B处的途中与灯塔P之间的最短距离为40√2海里.
(2)海轮以每小时30海里的速度从A处到B处,海轮不能在5小时内到达B处,理由如下:
∵∠PCB=90°,∠B=30°,
∴BC=√3PC=40√6(海里),
∴AB=AC+BC=(40√2+40√6)(海里),
∴海轮以每小时30海里的速度从A处到B处所用的时间=(40√2+40√6)/30=(4√2+4√6)/3≈(4×1.41+4×2.45)/3≈5.15(小时)＞5小时,
∴海轮以每小时30海里的速度从A处到B处,海轮不能在5小时内到达B处.

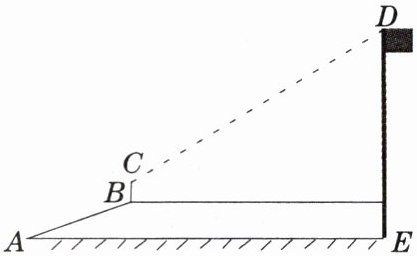
7. 某数学小组开展了一次测量学校旗杆高度的活动。如图,该数学小组从地面 $ A $ 处出发,沿坡角为 $ 24^{\circ} $ 的台阶 $ AB $ 上行到达点 $ B $ 处,再在点 $ B $ 处用测角仪测得旗杆顶端的仰角为 $ 50^{\circ} $,通过测量得知台阶斜面 $ AB $ 的长为 5 米,$ B $ 点到旗杆的距离为 10 米。已知测角仪高 1.6 米,求旗杆顶端离地面的高度 $ DE $。(结果精确到 1m,参考数据：$ \sin24^{\circ}\approx0.41 $,$ \cos24^{\circ}\approx0.91 $,$ \tan24^{\circ}\approx0.45 $,$ \sin50^{\circ}\approx0.77 $,$ \cos50^{\circ}\approx0.64 $,$ \tan50^{\circ}\approx1.19 $)

答案： 解:如图所示:过B作BG⊥AE,过C作CN⊥DE,
在Rt△AGB中,
∠AGB=90°,∠A=24°
∵AB=5m,
sin24°=BG/5,BG=0.41×5=2.05(m),
在Rt△CND中,∠CND=90°,∠DCN=50°,
CN=BM=10m,
∴tan50°=DN/10,DN=10×1.19=11.9(m)
∴DE=11.9+1.6+2.05=15.55(m)≈16(m)
答:旗杆顶端离地面的高度约为16米.

8. 自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图 1 所示的坡路进行改造。如图 2 所示,改造前的斜坡 $ AB = 200 $ 米,坡度为 $ 1:\sqrt{3} $；将斜坡 $ AB $ 的高度 $ AE $ 降低 $ AC = 20 $ 米后,斜坡 $ AB $ 改造为斜坡 $ CD $,其坡度为 $ 1:4 $。求斜坡 $ CD $ 的长。(结果保留根号)

答案： 解:
∵∠AEB=90°,AB=200,坡度为1:√3,
∴tan∠ABE=1/√3=√3/3,
∴∠ABE=30°,
∴AE=1/2AB=100.
∵AC=20,
∴CE=80.
∵∠CED=90°,斜坡CD的坡度为1:4,
∴CE/DE=1/4,即80/ED=1/4,
解得ED=320,
∴CD=√(80²+320²)=80√17(米),
答:斜坡CD的长是80√17米.