《2025年学习之友九年级数学上册北师大版》

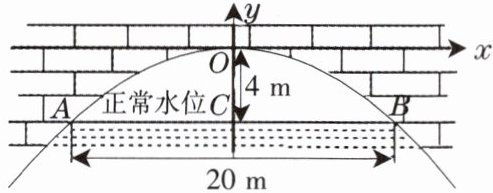
8. 有一座抛物线形拱桥,正常水位时桥下水面宽度为 $ 20 \, m $,拱顶距离水面 $ 4 \, m $.
(1)在如图所示的直角坐标系中,求出该抛物线的解析式;
(2)设正常水位时桥下的水深为 $ 2 \, m $,为保证过往船只顺利航行,桥下水面的宽度不得小于 $ 18 \, m $,求水深超过多少米时就会影响过往船只在桥下的顺利航行.

答案： 8.解:
(1)设该抛物线的解析式是$y = ax^{2}$，结合图象，把$(10,-4)$代入，得$100a = -4$，$a = -\frac{1}{25}$，则该抛物线的解析式是$y = -\frac{1}{25}x^{2}$.
(2)当$x = 9$时，则有$y = -\frac{1}{25}×81 = -3.24$，$4 + 2 - 3.24 = 2.76$(米).所以水深超过$2.76$米时就会影响过往船只在桥下的顺利航行.

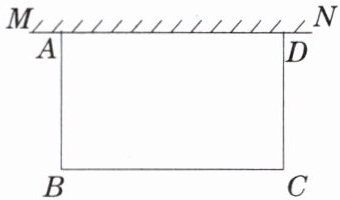
9. 如图,在足够大的空地上有一段长为 $ a $ 米的旧墙 $ MN $,某人利用旧墙和木栏围成一个矩形菜园 $ ABCD $,其中 $ AD \leq MN $,已知矩形菜园的一边靠墙,另三边一共用了 $ 100 $ 米木栏.
(1)若 $ a = 20 $,所围成的矩形菜园的面积为 $ 450 $ 平方米,求所利用旧墙 $ AD $ 的长;
(2)求矩形菜园 $ ABCD $ 面积的最大值.

答案： 9.解:
(1)设$AB = xm$，则$BC = (100 - 2x)m$，根据题意得$x(100 - 2x)=450$，解得$x_{1} = 5$，$x_{2} = 45$，当$x = 5$时，$100 - 2x = 90 ＞ 20$，不合题意舍去；当$x = 45$时，$100 - 2x = 10$，答：$AD$的长为$10m$.
(2)设$AD = xm$，$\therefore S=\frac{1}{2}x(100 - x)=-\frac{1}{2}(x - 50)^{2}+1250$，当$a\geq50$时，则$x = 50$时，$S$的最大值为$1250$；当$0 ＜ a ＜ 50$时，则当$0 ＜ x\leq a$时，$S$随$x$的增大而增大，当$x = a$时，$S$的最大值为$50a-\frac{1}{2}a^{2}$，综上所述，当$a\geq50$时，$S$的最大值为$1250$；当$0 ＜ a ＜ 50$时，$S$的最大值为$50a-\frac{1}{2}a^{2}$.

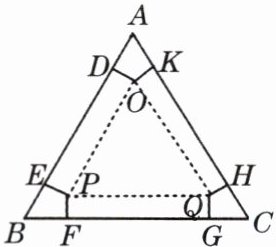
10. 如图,有一块边长为 $ 6 $ 的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝行,再沿图中虚线折起,做成一个无盖的直三棱柱纸盒,求纸盒侧面积的最大值多少?

答案： 10.解:如图，$\because\triangle ABC$为等边三角形，$\therefore\angle A = \angle B = \angle C = 60^{\circ}$，$AB = BC = AC$.$\because$筝形$ADOK\cong$筝形$BEPF\cong$筝形$CGQH$，$\therefore AD = BE = BF = CG = CH = AK$.$\because$折叠后是一个三棱柱，$\therefore DO = PE = PF = QG = QH = OK$，四边形$ODEP$、四边形$PFGQ$、四边形$QHKO$都为矩形.$\therefore\angle ADO = \angle AKO = 90^{\circ}$.连接$AO$，在$Rt\triangle AOD$和$Rt\triangle AOK$中，$\begin{cases}AO = AO\\OD = OK\end{cases}$$\therefore Rt\triangle AOD\cong Rt\triangle AOK(HL)$.$\therefore\angle OAD = \angle OAK = 30^{\circ}$.设$OD = x$，则$AO = 2x$，由勾股定理就可以求出$AD = \sqrt{3}x$，$\therefore DE = 6 - 2\sqrt{3}x$，$\therefore$纸盒侧面积$=3×(6 - 2\sqrt{3}x)= -6\sqrt{3}x^{2}+18x = -6\sqrt{3}(x - \frac{\sqrt{3}}{2})^{2}+\frac{9\sqrt{3}}{2}$，$\therefore$当$x = \frac{\sqrt{3}}{2}$时，纸盒侧面积最大为$\frac{9\sqrt{3}}{2}$.