《2025年学习之友九年级数学上册北师大版》

1. 某一时刻,身高 $1.6$ m 的小明在阳光下的影长是 $0.4$ m,同一时刻同一地点测得某旗杆的影长是 $5$ m,则该旗杆的高度是(C)。
A.$1.25$ m
B.$10$ m
C.$20$ m
D.$8$ m

答案： C

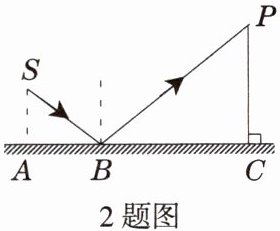
2. 如图,有一点光源 $S$ 在平面镜上方,若在点 $P$ 看到点光源的反射光线,并测得 $AB = 10$ cm,$BC = 20$ cm,$PC\perp AC$,且 $PC = 24$ cm,则点光源 $S$ 到平面镜的距离即 $SA$ 的长度为(B)。

A.$11$ cm
B.$12$ cm
C.$13$ cm
D.$14$ cm

答案： B

3. 如图,测量小玻璃管口径的量具 $ABC$ 上,$AB$ 的长为 $10$ mm,$AC$ 被分为 $60$ 等份。如果小管口 $DE$ 正好对着量具上 $30$ 份处($DE// AB$),那么小管口径 $DE$ 的长是(D)。
A.$5.6$ mm
B.$5.5$ mm
C.$5.8$ mm
D.$5$ mm

答案： D

4. 小李用长为 $4$ m 的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点。此时,竹竿与这一点相距 $8$ m,与旗杆相距 $22$ m,则旗杆的高为(B)。

A.$11$ m
B.$15$ m
C.$30$ m

D.$60$ m

答案： B

5. 小明从路灯下向前走了 $5$ m,发现自己在地面上的影子长 $DE$ 是 $2$ m。如果小明的身高为 $1.6$ m,那么路灯离地面的高度 $AB$ 是5.6m。

答案： 5.6

6. 我们知道：在同一时刻物高与影长成比例,某数学兴趣小组利用这一知识进行实地测量,其中一部分同学在某一时刻测得长为 $1$ m 的竹竿的影长是 $0.9$ m；另一部分同学在同一时刻对树影进行测量,可惜树太靠近一幢建筑物,树影不完全落在地面上,有一部分树影落在建筑物的墙壁上,如图所示,只测得地面上的树影长为 $2.7$ m。
(1)若设树高为 $y$ m,树在墙壁上的影高为 $x$ m,请你给出计算树高的表达式；
(2)如果树高为 $5$ m,那么此时留在墙壁上的树影有多高？

答案： 解:
(1)过点C作CE⊥AB于点E
由题意可知
$\frac{AE}{BD}=\frac{1}{0.9}$，即$\frac{y - x}{2.7}=\frac{1}{0.9}$，
$\therefore y = 3 + x$;
(2)若树高为5m，则由$y = 3 + x$得
$5 = 3 + x$，
解得$x = 2$.
答:此时留在墙壁上的树影有2m.

1. 要测量出一棵树的高度,除了测量出人高与人的影长外,还需要测出(B)。
A.仰角
B.树的影长
C.标杆的影长
D.都不需要

答案： B