第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
8. 如图,点 $ A,B,C,D $ 为矩形的四个顶点,$ AB= 16 cm $,$ AD= 6 cm $,动点 $ P,Q $ 分别从点 $ A,C $ 同时出发,点 $ P $ 以 $ 3 cm/s $ 的速度向点 $ B $ 移动,一直到达 $ B $ 点为止,点 $ Q $ 以 $ 2 cm/s $ 的速度向点 $ D $ 移动.
(1) 点 $ P,Q $ 两点从出发开始经过几秒钟,四边形 $ PBCQ $ 的面积为 $ 33 cm^{2} $;
(2) $ P,Q $ 两点从出发开始经过几秒钟,点 $ P $ 和点 $ Q $ 的距离为 $ 10 cm $?

(1) 点 $ P,Q $ 两点从出发开始经过几秒钟,四边形 $ PBCQ $ 的面积为 $ 33 cm^{2} $;
(2) $ P,Q $ 两点从出发开始经过几秒钟,点 $ P $ 和点 $ Q $ 的距离为 $ 10 cm $?

答案:
解:
(1)设x秒后四边形PBCQ的面积为$33cm^{2},$
则$\frac {1}{2}(16 - 3x + 2x)×6 = 33,$
解得$x = 5.$
(2)过点P作$PN⊥CD$于点N,设经过t秒钟后点P和Q相距10 cm,
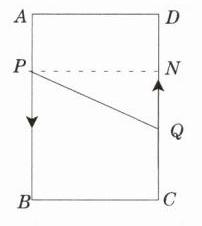
则$CQ = 2tcm,AP = DN = 3tcm$
$\therefore NQ = |CD - DN - CQ| = |16 - 3t - 2t| = |16 - 5t|$
在$Rt△PNQ$中,$PN^{2}+NQ^{2}+PQ^{2}$
$\therefore 22+(16 - 5t)^{2}=10^{2}$
$\therefore t_{1}=\frac {8}{5},t_{2}=\frac {24}{5}$即$t=\frac {8}{5}$秒或$\frac {24}{5}$秒时,$PQ = 10cm.$
解:
(1)设x秒后四边形PBCQ的面积为$33cm^{2},$
则$\frac {1}{2}(16 - 3x + 2x)×6 = 33,$
解得$x = 5.$
(2)过点P作$PN⊥CD$于点N,设经过t秒钟后点P和Q相距10 cm,

则$CQ = 2tcm,AP = DN = 3tcm$
$\therefore NQ = |CD - DN - CQ| = |16 - 3t - 2t| = |16 - 5t|$
在$Rt△PNQ$中,$PN^{2}+NQ^{2}+PQ^{2}$
$\therefore 22+(16 - 5t)^{2}=10^{2}$
$\therefore t_{1}=\frac {8}{5},t_{2}=\frac {24}{5}$即$t=\frac {8}{5}$秒或$\frac {24}{5}$秒时,$PQ = 10cm.$
9. 茶博物馆每周都吸引大量中外游客前来参观,若游客过多,对馆中的文物会不利,但同时考虑到文物的保存费用问题,还要保证一定的门票收入,因此博物馆采取提高门票价格的方法来控制人数,在该方法的实施过程中发现每周参观人数 $ y $(人)与票价 $ x $(元)之间存在着如图所示的一次函数关系,在这种情况下,若要保证每周 4 万元的门票收入,那么每周应限定参观人数为多少?


答案:
解:由题意得$y = - 500x + 12000(x > 0),$
$\because xy = 40000,$
$\therefore x(-500x + 12000)=40000,$
即$x^{2}-24x + 80 = 0,$
解得$x_{1}=20,x_{2}=4$,分别代入$y = - 500x + 12000,$
解得$y_{1}=2000,y_{2}=10000.$
由于要控制人数,所以取$x = 20$,此时$y = 2000.$
答:每周应限定参观人数为2000人,门票价格是20元.
$\because xy = 40000,$
$\therefore x(-500x + 12000)=40000,$
即$x^{2}-24x + 80 = 0,$
解得$x_{1}=20,x_{2}=4$,分别代入$y = - 500x + 12000,$
解得$y_{1}=2000,y_{2}=10000.$
由于要控制人数,所以取$x = 20$,此时$y = 2000.$
答:每周应限定参观人数为2000人,门票价格是20元.
查看更多完整答案,请扫码查看


