第69页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
1. (教材九上 P52“阅读与思考”变式)某航空公司对某型号飞机进行着陆后的滑行测试. 飞机着陆后滑行的距离 $ s(m) $ 关于游行的时间 $ t(s) $ 的函数解析式是 $ s = -\dfrac{3}{2}t^{2} + 60t $,则 $ t $ 的取值范围是(
A.$ 0 \leqslant t \leqslant 600 $
B.$ 20 \leqslant t \leqslant 40 $
C.$ 0 \leqslant t \leqslant 40 $
D.$ 0 \leqslant t \leqslant 20 $
D
)A.$ 0 \leqslant t \leqslant 600 $
B.$ 20 \leqslant t \leqslant 40 $
C.$ 0 \leqslant t \leqslant 40 $
D.$ 0 \leqslant t \leqslant 20 $
答案:
1.D
2. 新考向 数学文化 (2021·广东)我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为 $ a $, $ b $, $ c $, 记 $ p = \dfrac{a + b + c}{2} $, 则其面积 $ S = \sqrt{p(p - a)(p - b)(p - c)} $. 这个公式也被称为“海伦—秦九韶公式”. 若 $ p = 5 $, $ c = 4 $, 则此三角形面积的最大值为(
A.$ \sqrt{5} $
B.4
C.$ 2\sqrt{5} $
D.5
C
)A.$ \sqrt{5} $
B.4
C.$ 2\sqrt{5} $
D.5
答案:
2.C
3. (教材九上 P48“信息技术应用”变式)计算机可以帮助我们又快又准地画出函数的图象. 用“几何画板”软件画出的函数 $ y = x^{2}(x + 3) $ 和 $ y = x + 3 $ 的图象如图所示. 根据图象可知方程 $ x^{2}(x + 3) = x + 3 $ 的解的个数为
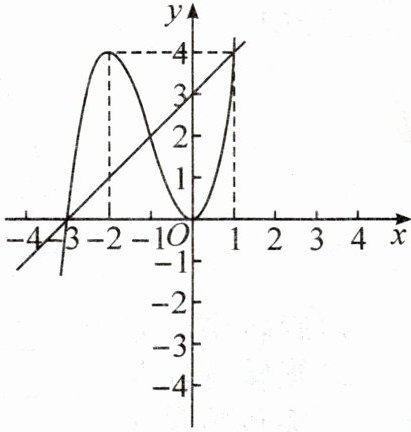
]
3
;若 $ m $, $ n $ 分别满足方程 $ x^{2}(x + 3) = 5 $ 和 $ x + 3 = 5 $, 则 $ m $, $ n $ 的大小关系是$m < n$
.
]
答案:
3.3 $m < n$
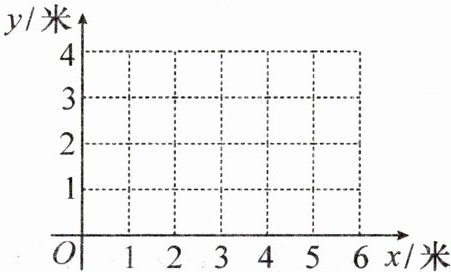
4. 新考向 情境素材 深圳市某景观公园计划修建一个人工喷泉,从垂直于地面的喷水枪喷出的水流路径可以看作是抛物线的一部分. 记喷出的水流距喷水枪的水平距离为 $ x $ 米,距地面的竖直高度为 $ y $ 米,获得数据如下表:

小华根据学习函数的经验,对函数 $ y $ 随自变量 $ x $ 的变化而变化的规律进行了探究. 下面是小华的探究过程,请补充完整:
(1) 在平面直角坐标系 $ xOy $ 中,描出以表中各组对应值为坐标的点,并用平滑曲线画出该函数的图象;
(2) 直接写出水流最高点距离地面的高度为_______米;
(3) 求该抛物线的解析式;(结果用一般式表示)
(4) 结合函数图象,解决问题:该景观公园准备在距喷水枪水平距离 3 米处修建一个大理石雕塑,使喷水枪喷出的水流刚好落在雕塑顶端,则大理石雕塑的高度约为_______米.(结果精确到 0.1 米)

小华根据学习函数的经验,对函数 $ y $ 随自变量 $ x $ 的变化而变化的规律进行了探究. 下面是小华的探究过程,请补充完整:
(1) 在平面直角坐标系 $ xOy $ 中,描出以表中各组对应值为坐标的点,并用平滑曲线画出该函数的图象;
(2) 直接写出水流最高点距离地面的高度为_______米;
(3) 求该抛物线的解析式;(结果用一般式表示)
(4) 结合函数图象,解决问题:该景观公园准备在距喷水枪水平距离 3 米处修建一个大理石雕塑,使喷水枪喷出的水流刚好落在雕塑顶端,则大理石雕塑的高度约为_______米.(结果精确到 0.1 米)

答案:
4.解:
(1)略.
(2)3
(3)设抛物线的解析式为$y=a(x-2)^2+3$,将$(5,0)$代入解析式,得$9a+3=0$,解得$a=-\dfrac{1}{3}$,
∴抛物线的解析式为$y=-\dfrac{1}{3}(x-2)^2+3=-\dfrac{1}{3}x^2+\dfrac{4}{3}x+\dfrac{5}{3}$.
(4)2.7
(1)略.
(2)3
(3)设抛物线的解析式为$y=a(x-2)^2+3$,将$(5,0)$代入解析式,得$9a+3=0$,解得$a=-\dfrac{1}{3}$,
∴抛物线的解析式为$y=-\dfrac{1}{3}(x-2)^2+3=-\dfrac{1}{3}x^2+\dfrac{4}{3}x+\dfrac{5}{3}$.
(4)2.7
5. (教材九上 P54“数学活动 2”变式)如图,在平面直角坐标系中,点 $ A $ 的坐标是 $ (0,2) $, 在 $ x $ 轴上任取一点 $ M $, 连接 $ AM $, 作线段 $ AM $ 的垂直平分线 $ l_{1} $, 过点 $ M $ 作 $ x $ 轴的垂线 $ l_{2} $, 记 $ l_{1} $, $ l_{2} $ 的交点为 $ P $.
(1) 线段 $ PA $ 与 $ PM $ 的数量关系为
① 当点 $ M $ 的坐标为 $ (2,0) $ 时,点 $ P $ 的坐标是
② 当点 $ M $ 的坐标为 $ (4,0) $ 时,点 $ P $ 的坐标是
(2) 在 $ x $ 轴上改变点 $ M $ 的位置,可得到不同的点 $ P $, 试着把得到的点 $ P $ 用平滑的曲线连接起来. 观察画出的曲线 $ L $, 猜想它是我们学过的哪种曲线:
(3) 验证(2)的猜想:对于曲线 $ L $ 上任意一点 $ P $, 设点 $ P $ 的坐标是 $ (x,y) $, 请根据 $ PA $ 与 $ PM $ 的关系求出 $ x $, $ y $ 满足的关系式. 你得出的结论与先前你的猜想一样吗?
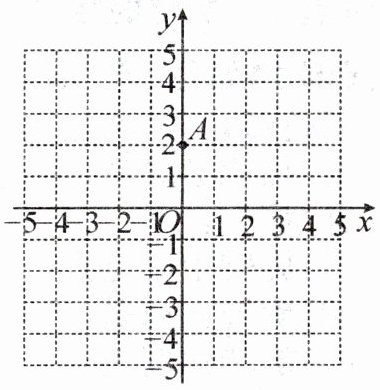
]
(1) 线段 $ PA $ 与 $ PM $ 的数量关系为
PA=PM
.① 当点 $ M $ 的坐标为 $ (2,0) $ 时,点 $ P $ 的坐标是
(2,2)
;② 当点 $ M $ 的坐标为 $ (4,0) $ 时,点 $ P $ 的坐标是
(4,5)
;(2) 在 $ x $ 轴上改变点 $ M $ 的位置,可得到不同的点 $ P $, 试着把得到的点 $ P $ 用平滑的曲线连接起来. 观察画出的曲线 $ L $, 猜想它是我们学过的哪种曲线:
抛物线
;(3) 验证(2)的猜想:对于曲线 $ L $ 上任意一点 $ P $, 设点 $ P $ 的坐标是 $ (x,y) $, 请根据 $ PA $ 与 $ PM $ 的关系求出 $ x $, $ y $ 满足的关系式. 你得出的结论与先前你的猜想一样吗?

]
答案:
5.解:
(1)$PA=PM$ ②$(2,2)$ ③$(4,5)$
(2)抛物线
(3)我得出的结论与先前我的猜想一样.理由如下:
∵点P的坐标是$(x,y)$,$PM\perp x$轴,
∴$M(x,0)$.
∵$A(0,2)$,$PA=PM$,$(x-0)^2+(y-2)^2=y^2$,
∴$x^2+y^2-4y+4=y^2$.化简,得$y=\dfrac{1}{4}x^2+1$.
∵$y=\dfrac{1}{4}x^2+1$为抛物线解析式,
∴得出的结论与猜想一致.
(1)$PA=PM$ ②$(2,2)$ ③$(4,5)$
(2)抛物线
(3)我得出的结论与先前我的猜想一样.理由如下:
∵点P的坐标是$(x,y)$,$PM\perp x$轴,
∴$M(x,0)$.
∵$A(0,2)$,$PA=PM$,$(x-0)^2+(y-2)^2=y^2$,
∴$x^2+y^2-4y+4=y^2$.化简,得$y=\dfrac{1}{4}x^2+1$.
∵$y=\dfrac{1}{4}x^2+1$为抛物线解析式,
∴得出的结论与猜想一致.
查看更多完整答案,请扫码查看


