《2025年名校课堂九年级数学全一册人教版广东专版》

5.【例2】已知反比例函数 $ y = \frac{6}{x} $.
(1)在每个象限内，$ y $ 随 $ x $ 的增大而减小；
(2)当 $ 2 \leq x \leq 6 $ 时，$ y $ 的取值范围是1≤y≤3.

答案： 5.
(1)减小
(2)1≤y≤3

6. 已知反比例函数 $ y = \frac{1 - k}{x} $ 的图象经过点 $ A(2,-4) $.
(1)反比例函数的解析式为$y=-\frac{8}{x}$；
(2)函数图象位于第二、四象限，在每个象限内，$ y $ 随 $ x $ 的增大而增大；
(3)当 $ 2 ＜ y ＜ 8 $ 时，自变量 $ x $ 的取值范围是-4＜x＜-1.

答案： 6.
(1)$y=-\frac{8}{x}$
(2)二、四 增大
(3)-4＜x＜-1

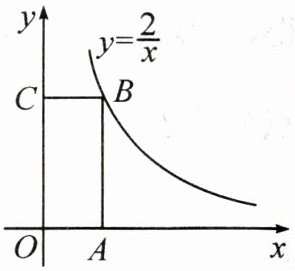
7.【例3】如图，点 $ B $ 在反比例函数 $ y = \frac{2}{x}(x ＞ 0) $ 的图象上，过点 $ B $ 分别向 $ x $ 轴、$ y $ 轴作垂线，垂足分别为点 $ A $，点 $ C $，则矩形 $ OABC $ 的面积为(B)

A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $

答案： 7.B

8. 如图，已知 $ A $ 为反比例函数 $ y = \frac{k}{x}(x ＜ 0) $ 的图象上一点，过点 $ A $ 作 $ AB \perp y $ 轴，垂足为 $ B $.若 $ \triangle OAB $ 的面积为 $ 3 $，则 $ k $ 的值为(D)

A.$ 3 $
B.$ -3 $
C.$ 6 $
D.$ -6 $

答案： 8.D

9. 已知 $ (x_1,y_1) $，$ (x_2,y_2) $ 是反比例函数 $ y = \frac{5}{x} $ 图象上的两点，且 $ 0 ＜ x_1 ＜ x_2 $，则 $ y_1 $，$ y_2 $ 的大小关系是(B)

A.$ 0 ＜ y_1 ＜ y_2 $
B.$ 0 ＜ y_2 ＜ y_1 $
C.$ y_1 ＜ y_2 ＜ 0 $
D.$ y_2 ＜ y_1 ＜ 0 $

答案： 9.B

10. 已知反比例函数 $ y = \frac{-2}{x} $ 的图象如图，$ P $，$ Q $ 为图象上任意两点，$ S_{\triangle OAP} $ 记为 $ S_1 $，$ S_{\triangle OBQ} $ 记为 $ S_2 $，则(A)


A.$ S_1 = S_2 $
B.$ S_1 ＞ S_2 $
C.$ S_1 ＜ S_2 $
D.无法判断

答案： 10.A

11. 已知反比例函数 $ y = \frac{3 - m}{x} $ 的图象过点 $ (-3,4) $.
(1)$ m = $15，反比例函数的解析式为$y=-\frac{12}{x}$；
(2)当 $ -1 \leq y \leq -6 $ 时，求 $ x $ 的取值范围.

答案： 11.解:
(1)15 $y=-\frac{12}{x}$
(2)对于反比例函数$y=-\frac{12}{x}$,在每个象限内,y随x的增大而增大.当y=-1时,x=12;当y=-6时,x=2.
∴当-1≤y≤-6时,x的取值范围是2≤x≤12.

12. (2024·东莞松山湖未来学校期末)如图，$ A $ 是反比例函数 $ y = \frac{k}{x} $ 的图象上的一点，过点 $ A $ 作 $ AB \perp x $ 轴，垂足为 $ B $，$ C $ 为 $ y $ 轴上的一点，连接 $ AC $，$ BC $.若 $ \triangle ABC $ 的面积为 $ 6 $，则 $ k $ 的值是-12.

答案： -12