《2025年亮点给力大试卷八年级数学上册苏科版》

18. 新素养 推理能力 如图,在平面直角坐标系中有一个点 $ P(1,0) $,点 $ P $ 第 1 次向上跳动 1 个单位长度至点 $ P_1(1,1) $,紧接着第 2 次向左跳动 2 个单位长度至点 $ P_2(-1,1) $,第 3 次向上跳动 1 个单位长度,第 4 次向右跳动 3 个单位长度,第 5 次向上跳动 1 个单位长度,第 6 次向左跳动 4 个单位长度,…,依此规律跳动下去,点 $ P $ 第 2025 次跳动至点 $ P_{2025} $ 的坐标为______.

答案： (507,1013)　解析:观察可知P₁(1,1)，P₅(2,3)，P₉(3,5)，P₁₃(4,7)，…，依此类推可知，点P₄ₙ₊₁的坐标为(n+1,2n+1)。因为2025=4×506+1，所以点P₂₀₂₅的坐标为(506+1,2×506+1)，即(507,1013)。

19. (6 分)如图,在 $ 10 × 10 $ 的正方形网格中,每个小正方形的边长都为 1,格点三角形 $ ABC $(顶点是网格线的交点)的顶点 $ A,C $ 在平面直角坐标系中的坐标分别为 $ (-4,3),(-1,1) $.
(1) 画出平面直角坐标系;
(2) 画出 $ \triangle ABC $ 关于 $ y $ 轴对称的 $ \triangle A'B'C' $;(点 $ A,B,C $ 的对应点分别为 $ A',B',C' $)
(3) 在 $ x $ 轴上确定一格点 $ P $,使得 $ \triangle PBC $ 为直角三角形,则满足条件的所有格点 $ P $ 的横坐标为-4，1.

答案： 1. 首先，根据$A(-4,3)$，$C(-1,1)$画出平面直角坐标系：
以点$A$向左$4$个单位，向下$3$个单位的交点为原点$O$，过原点$O$作水平向右的$x$轴和垂直向上的$y$轴。
2. 然后，求$B$点坐标并画出$\triangle A'B'C'$：
由网格可得$B(-2,-1)$。
根据关于$y$轴对称的点的坐标特征：点$(x,y)$关于$y$轴对称的点的坐标为$(-x,y)$。
已知$A(-4,3)$，则$A'$的坐标为$(4,3)$；$B(-2,-1)$，则$B'$的坐标为$(2,-1)$；$C(-1,1)$，则$C'$的坐标为$(1,1)$。连接$A'B'$，$B'C'$，$A'C'$，得到$\triangle A'B'C'$。
3. 最后，求满足条件的$P$点横坐标：
设$P(x,0)$，根据勾股定理$a^{2}+b^{2}=c^{2}$（其中$a$，$b$为直角边，$c$为斜边）。
已知$B(-2,-1)$，$C(-1,1)$，则$BC^{2}=(-1 + 2)^{2}+(1 + 1)^{2}=1 + 4=5$，$PB^{2}=(x + 2)^{2}+(0 + 1)^{2}=(x + 2)^{2}+1=x^{2}+4x+4 + 1=x^{2}+4x+5$，$PC^{2}=(x + 1)^{2}+(0 - 1)^{2}=(x + 1)^{2}+1=x^{2}+2x+1 + 1=x^{2}+2x+2$。
分三种情况讨论：
当$\angle BPC = 90^{\circ}$时，$PB^{2}+PC^{2}=BC^{2}$，即$x^{2}+4x+5+x^{2}+2x+2 = 5$。
化简得$2x^{2}+6x + 2 = 0$，$x^{2}+3x + 1 = 0$，$x=\frac{-3\pm\sqrt{9 - 4}}{2}=\frac{-3\pm\sqrt{5}}{2}$（舍去，因为$P$是格点）。
当$\angle PBC = 90^{\circ}$时，$PB^{2}+BC^{2}=PC^{2}$，即$x^{2}+4x+5 + 5=x^{2}+2x+2$。
化简得$x^{2}+4x+10=x^{2}+2x+2$，移项得$4x-2x=2 - 10$，$2x=-8$，解得$x=-4$。
当$\angle PCB = 90^{\circ}$时，$PC^{2}+BC^{2}=PB^{2}$，即$x^{2}+2x+2 + 5=x^{2}+4x+5$。
化简得$x^{2}+2x+7=x^{2}+4x+5$，移项得$2x=2$，解得$x = 1$。
所以满足条件的所有格点$P$的横坐标为$-4$，$1$。

20. (6 分)八(2)班学生共有 48 人,班上座位是安排 8 列 6 排,进门一列为第 1 列,靠讲台一排为第 1 排.
(1) 若用 $ A_{12} $ 表示第 1 列第 2 排,则 $ A_{56} $ 表示的是什么位置?
(2) 若排列号调换后是两个不同位置,则称位置受排列号影响. 你认为班上有几个位置不受排列号影响? 请把它们写出来.

答案：
(1)A₅₆表示的是第5列第6排。
(2)班上有6个位置不受排列号影响，它们分别为A₁₁,A₂₂,A₃₃,A₄₄,A₅₅,A₆₆。

21. (6 分)如图,在平面直角坐标系中,$ O $ 是原点,已知点 $ A(-1,0),C(1,4) $,点 $ B $ 在 $ x $ 轴上,且 $ AB = 3 $.

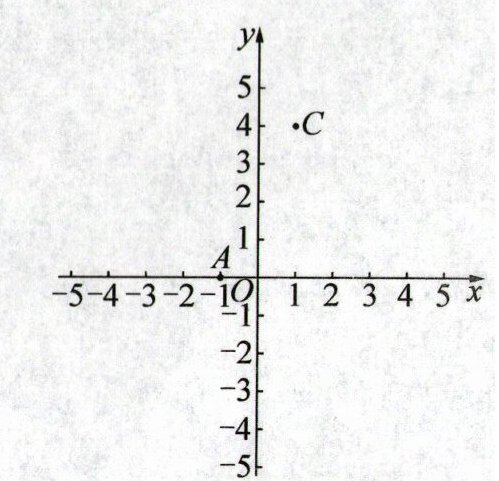
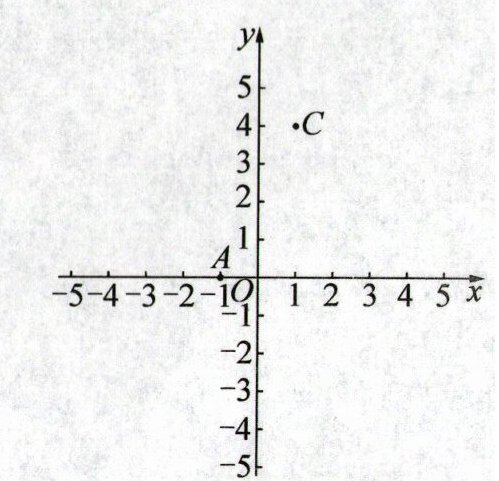
(1) 求点 $ B $ 的坐标,并画出 $ \triangle ABC $;
(2) 求 $ \triangle ABC $ 的面积;
(3) 在 $ y $ 轴上是否存在点 $ P $,使以 $ A,B,P $ 三点为顶点的三角形的面积为 10? 若存在,请求出点 $ P $ 的坐标;若不存在,请说明理由.

答案：
(1)因为A(−1,0)，所以OA=1。因为AB=3，所以分类讨论如下:①当点B在点A左侧时，OB=OA+AB=4，所以B(−4,0);②当点B在点A右侧时，OB=AB - OA=2，所以B(2,0)。综上所述，点B的坐标为(−4,0)或(2,0)。图略。
(2)过点C作CD⊥x轴于点D。因为C(1,4)，所以CD=4。因为AB=3，所以S△ABC=1/2AB·CD=6。故△ABC的面积为6。
(3)因为点P在y轴上，所以PO⊥AB，所以S△ABP=1/2AB·PO。因为S△ABP=10，AB=3，所以PO=10×2/3=20/3，所以点P的坐标为(0,20/3)或(0,−20/3)。故存在满足题意的点P，且点P的坐标为(0,20/3)或(0,−20/3)。

22. (4 分)新素养 几何直观 如图,在平面直角坐标系中,四边形 $ OABC $ 各顶点的坐标分别是 $ O(0,0),A(2,3),B(5,4),C(8,2) $,求四边形 $ OABC $ 的面积.

答案： 由题意，得S四边形OABC=8×4 - 1/2×2×3 - 1/2×2×8 - 1/2×(8 - 5)×(4 - 2) - 1/2×(2 + 5)×(4 - 3)=14.5。故四边形OABC的面积为14.5。