第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
7. 如图,在$Rt\triangle ABC$中,$∠ACB = 90^{\circ}$,$AB = 13$,$AC = 5$,动点 P 从点 B 出发沿射线 BC 以每秒 2 个单位长度的速度运动.设运动的时间为 t s,则当$\triangle APB$为等腰三角形时,t 的值为 (
A.$\frac{169}{48}或\frac{13}{2}$
B.$\frac{13}{2}$或 12 或 4
C.$\frac{13}{2}$或 12 或$\frac{169}{48}$
D.$\frac{169}{48}$或 12 或 4
C
)A.$\frac{169}{48}或\frac{13}{2}$
B.$\frac{13}{2}$或 12 或 4
C.$\frac{13}{2}$或 12 或$\frac{169}{48}$
D.$\frac{169}{48}$或 12 或 4
答案:
C 解析:由题意,得BP=2t.因为∠ACB=90°,AB=13,AC=5,所以BC=√(AB² - AC²)=12.当△APB为等腰三角形时,分类讨论如下:①若BP=AB,则2t=13,解得t=13/2;②若AP=AB,则BP=2BC=24,所以2t=24,解得t=12;③若AP=BP=2t,则CP=BC - BP=12 - 2t.因为AC²+CP²=AP²,所以5²+(12 - 2t)²=(2t)²,解得t=169/48.综上所述,t的值为13/2或12或169/48.
8. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按如图②所示的方式放置在最大的正方形内.若知道图②中阴影部分的面积,则一定能求出 (
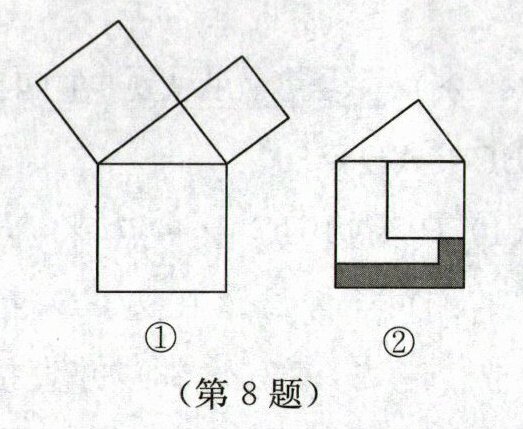
A.直角三角形的面积
B.最大正方形的面积
C.较小的两个正方形重叠部分的面积
D.最大的正方形与直角三角形的面积和
C
)
A.直角三角形的面积
B.最大正方形的面积
C.较小的两个正方形重叠部分的面积
D.最大的正方形与直角三角形的面积和
答案:
C 解析:设题图①中直角三角形的两直角边长分别为a,b(a>b),斜边长为c,则a²+b²=c².题图②中阴影部分的面积可表示为c² - a² - b(c - a)=b² - bc + ab=b(a + b - c),较小的两个正方形重叠部分的面积可表示为b[a - (c - b)]=b(a + b - c),所以较小的两个正方形重叠部分的面积等于阴影部分的面积.
9. 若直角三角形的一条直角边长与斜边长分别为 6 cm 和 10 cm,则该直角三角形斜边上的中线长为
5
cm,斜边上的高为4.8
cm.
答案:
5 4.8
10. 在$\triangle ABC$中,已知 a,b,c 分别为$∠A$,$∠B$,$∠C$所对边的长.若$a^{2} + b^{2} = 25$,$a^{2} - b^{2} = 7$,$c = 5$,则$\triangle ABC$最长边上的高为______
2.4
.
答案:
2.4
11. (2023·江苏南通)勾股数是指能成为直角三角形三边长的三个正整数,世界上第一次给出勾股数公式的是我国古代数学著作《九章算术》.现有勾股数 a,b,c,其中 a,b 均小于 c,且$a = \frac{1}{2}m^{2} - \frac{1}{2}$,$c = \frac{1}{2}m^{2} + \frac{1}{2}$(m 是大于 1 的奇数),则$b = $
m
.(用含 m 的代数式表示)
答案:
m
12. 如图,$CB⊥AD$,$AE⊥CD$,垂足分别为 B,E,AE,CB 相交于点 F,$AB = CB$.若$AB = 8$,$CF = 2$,则$CD = $
10
.
答案:
10
13. 新趋势 情境素材 如图,某港口 P 位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行 12 海里和 16 海里,1 h 后两船分别位于点 A,B 处,且相距 20 海里.若知道甲船沿北偏西$40^{\circ}$方向航行,则乙船沿
北偏东50°
方向航行.
答案:
北偏东50°
14. (2025·江苏常州模拟)如图,在$\triangle ABC$中,$∠ABC$,$∠ACB$的平分线相交于点 O,$OD⊥BC$于点 D.若$AB = 25$cm,$BC = 20$cm,$AC = 15$cm,则$OD = $
5
cm.
答案:
5
15. 如图,$AB⊥BC$,$AB⊥AD$,E 是 CD 的中点.若$BC = 5$,$AD = 10$,$BE = \frac{13}{2}$,则$AB = $
12
.
答案:
12
查看更多完整答案,请扫码查看


