第114页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
28. (8分)新趋势 推导探究
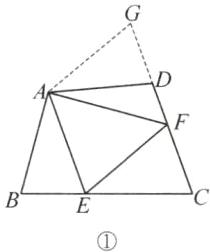
【问题背景】如图①,在四边形ABCD中,$AB= AD,∠BAD= 120^{\circ },∠ABC= ∠ADC= 90^{\circ }$,E,F分别是边BC,CD上的点,且$∠EAF= 60^{\circ }$,探究线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法如下:延长FD到点G,使$DG= BE$,连接AG,先证明$△ABE\cong △ADG$,再证明$△AEF\cong △AGF$,可得到正确结论.他的结论是______.
【探索延伸】如图②,在四边形ABCD中,$AB= AD,∠ABC+∠ADC= 180^{\circ }$,E,F分别是边BC,CD上的点,且$∠EAF= \frac {1}{2}∠BAD$,上述结论是否仍然成立? 并说明理由.
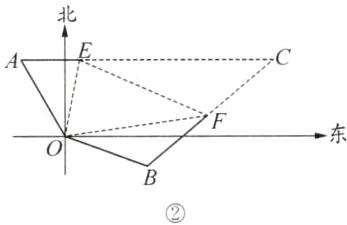
【结论应用】如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西$30^{\circ }$的A处,舰艇乙在指挥中心南偏东$70^{\circ }$的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60 n mile/h的速度前进,舰艇乙沿北偏东$50^{\circ }$的方向以80 n mile/h的速度前进,1.5 h后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间的夹角$∠EOF= 70^{\circ }$,试求此时两舰艇之间的距离.
【能力提高】如图④,在$△ABC$中,$∠BAC= 90^{\circ },AB= AC$,点M,N在边BC上,且$∠MAN= 45^{\circ }$.若$BM= 1,CN= 3$,则MN的长为______.

【问题背景】如图①,在四边形ABCD中,$AB= AD,∠BAD= 120^{\circ },∠ABC= ∠ADC= 90^{\circ }$,E,F分别是边BC,CD上的点,且$∠EAF= 60^{\circ }$,探究线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法如下:延长FD到点G,使$DG= BE$,连接AG,先证明$△ABE\cong △ADG$,再证明$△AEF\cong △AGF$,可得到正确结论.他的结论是______.
【探索延伸】如图②,在四边形ABCD中,$AB= AD,∠ABC+∠ADC= 180^{\circ }$,E,F分别是边BC,CD上的点,且$∠EAF= \frac {1}{2}∠BAD$,上述结论是否仍然成立? 并说明理由.
【结论应用】如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西$30^{\circ }$的A处,舰艇乙在指挥中心南偏东$70^{\circ }$的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60 n mile/h的速度前进,舰艇乙沿北偏东$50^{\circ }$的方向以80 n mile/h的速度前进,1.5 h后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间的夹角$∠EOF= 70^{\circ }$,试求此时两舰艇之间的距离.
【能力提高】如图④,在$△ABC$中,$∠BAC= 90^{\circ },AB= AC$,点M,N在边BC上,且$∠MAN= 45^{\circ }$.若$BM= 1,CN= 3$,则MN的长为______.

答案:
[问题背景]EF = BE + FD
[探索延伸]EF = BE + FD仍然成立。理由如下:如图①,延长FD到点G,使DG = BE,连接AG。因为$∠ABC + ∠ADC = 180^{\circ }$,$∠ADG + ∠ADC = 180^{\circ }$,所以$∠B = ∠ADG$。在△ABE和△ADG中,$\left\{\begin{array}{l} AB=AD,\\ ∠B=∠ADG,\\ BE=DG,\end{array}\right. $所以$△ABE\cong △ADG$(SAS),所以AE = AG,$∠BAE = ∠DAG$因为$∠EAF=\frac {1}{2}∠BAD$,所以$∠GAF = ∠FAD + ∠DAG = ∠FAD + ∠BAE = ∠BAD - ∠EAF=\frac {1}{2}∠BAD$,所以$∠EAF = ∠GAF$。在△AEF和△AGF中,$\left\{\begin{array}{l} AE=AG,\\ ∠EAF=∠GAF,\\ AF=AF,\end{array}\right. $所以$△AEF\cong △AGF$(SAS),所以EF = GF。因为GF = DG + FD = BE + FD,所以EF = BE + FD。
[结论应用]如图②,连接EF,分别延长AE,BF相交于点C。在四边形AOBC中,因为$∠AOB = 30^{\circ } + 90^{\circ } + (90^{\circ } - 70^{\circ })=140^{\circ }$,$∠EOF = 70^{\circ }$,所以$∠EOF=\frac {1}{2}∠AOB$。又OA = OB,$∠OAC + ∠OBC = 90^{\circ } - 30^{\circ } + 70^{\circ } + 50^{\circ } = 180^{\circ }$,符合[探索延伸]中的条件,所以结论EF = AE + BF成立。因为AE = 60×1.5 = 90(n mile),BF = 80×1.5 = 120(n mile),所以EF = 210n mile。故此时两舰艇之间的距离为210n mile。
[能力提高]$\sqrt{10}$ 解析:如图③,在△ABC外侧作$∠CAD = ∠BAM$,截取AD = AM,连接CD,DN。因为$∠BAC = 90^{\circ }$,AB = AC,所以$∠B = ∠ACB=\frac {1}{2}(180^{\circ } - ∠BAC)=45^{\circ }$。在△ACD和△ABM中,$\left\{\begin{array}{l} AC=AB,\\ ∠CAD=∠BAM,\\ AD=AM,\end{array}\right. $所以$△ACD\cong △ABM$(SAS),所以CD = BM = 1,$∠ACD = ∠B = 45^{\circ }$,所以$∠NCD = ∠ACB + ∠ACD = 90^{\circ }$。因为CN = 3,所以DN = $\sqrt{CN^{2}+CD^{2}}=\sqrt{10}$。因为$∠MAN = 45^{\circ }$,所以$∠BAM + ∠CAN = ∠BAC - ∠MAN = 45^{\circ }$,所以$∠CAD + ∠CAN = 45^{\circ }$,所以$∠DAN = 45^{\circ }$,所以$∠MAN = ∠DAN$。在△MAN和△DAN中,$\left\{\begin{array}{l} AM=AD,\\ ∠MAN=∠DAN,\\ AN=AN,\end{array}\right. $所以$△MAN\cong △DAN$(SAS),所以MN = DN = $\sqrt{10}$。

[问题背景]EF = BE + FD
[探索延伸]EF = BE + FD仍然成立。理由如下:如图①,延长FD到点G,使DG = BE,连接AG。因为$∠ABC + ∠ADC = 180^{\circ }$,$∠ADG + ∠ADC = 180^{\circ }$,所以$∠B = ∠ADG$。在△ABE和△ADG中,$\left\{\begin{array}{l} AB=AD,\\ ∠B=∠ADG,\\ BE=DG,\end{array}\right. $所以$△ABE\cong △ADG$(SAS),所以AE = AG,$∠BAE = ∠DAG$因为$∠EAF=\frac {1}{2}∠BAD$,所以$∠GAF = ∠FAD + ∠DAG = ∠FAD + ∠BAE = ∠BAD - ∠EAF=\frac {1}{2}∠BAD$,所以$∠EAF = ∠GAF$。在△AEF和△AGF中,$\left\{\begin{array}{l} AE=AG,\\ ∠EAF=∠GAF,\\ AF=AF,\end{array}\right. $所以$△AEF\cong △AGF$(SAS),所以EF = GF。因为GF = DG + FD = BE + FD,所以EF = BE + FD。

[结论应用]如图②,连接EF,分别延长AE,BF相交于点C。在四边形AOBC中,因为$∠AOB = 30^{\circ } + 90^{\circ } + (90^{\circ } - 70^{\circ })=140^{\circ }$,$∠EOF = 70^{\circ }$,所以$∠EOF=\frac {1}{2}∠AOB$。又OA = OB,$∠OAC + ∠OBC = 90^{\circ } - 30^{\circ } + 70^{\circ } + 50^{\circ } = 180^{\circ }$,符合[探索延伸]中的条件,所以结论EF = AE + BF成立。因为AE = 60×1.5 = 90(n mile),BF = 80×1.5 = 120(n mile),所以EF = 210n mile。故此时两舰艇之间的距离为210n mile。

[能力提高]$\sqrt{10}$ 解析:如图③,在△ABC外侧作$∠CAD = ∠BAM$,截取AD = AM,连接CD,DN。因为$∠BAC = 90^{\circ }$,AB = AC,所以$∠B = ∠ACB=\frac {1}{2}(180^{\circ } - ∠BAC)=45^{\circ }$。在△ACD和△ABM中,$\left\{\begin{array}{l} AC=AB,\\ ∠CAD=∠BAM,\\ AD=AM,\end{array}\right. $所以$△ACD\cong △ABM$(SAS),所以CD = BM = 1,$∠ACD = ∠B = 45^{\circ }$,所以$∠NCD = ∠ACB + ∠ACD = 90^{\circ }$。因为CN = 3,所以DN = $\sqrt{CN^{2}+CD^{2}}=\sqrt{10}$。因为$∠MAN = 45^{\circ }$,所以$∠BAM + ∠CAN = ∠BAC - ∠MAN = 45^{\circ }$,所以$∠CAD + ∠CAN = 45^{\circ }$,所以$∠DAN = 45^{\circ }$,所以$∠MAN = ∠DAN$。在△MAN和△DAN中,$\left\{\begin{array}{l} AM=AD,\\ ∠MAN=∠DAN,\\ AN=AN,\end{array}\right. $所以$△MAN\cong △DAN$(SAS),所以MN = DN = $\sqrt{10}$。

查看更多完整答案,请扫码查看


