《2025年亮点给力大试卷八年级数学上册苏科版》

26. (8分)新素养 推理能力
【感知】如图①,点B,A,C在同一条直线上,$DB⊥BC,EC⊥BC$,且$∠DAE= 90^{\circ },DA= AE$,易证$△DBA\cong △ACE$.(不必证明)
【探究】如图②,在$△DBA和△ACE$中,$DA= AE$.若$∠DAE= α(0^{\circ }＜α＜90^{\circ }),∠BAC= 2α,∠B= ∠C= 180^{\circ }-α$,求证:$△DBA\cong △ACE$.
【应用】如图②,在$△DBA和△ACE$中,$DA= AE$.若$∠DAE= 70^{\circ },∠BAC= 140^{\circ },∠B= ∠C= 110^{\circ }$,则当$∠D$为多少度时,$∠DAC的度数是∠E$的3倍?

答案： [探究]因为$∠BAC = 2α$，$∠DAE = α$，所以$∠DAB + ∠EAC = ∠BAC - ∠DAE = α$。因为$∠B = 180^{\circ } - α$，所以$∠DAB + ∠D = 180^{\circ } - ∠B = α$，所以$∠D = ∠EAC$。在△DBA和△ACE中，$\left\{\begin{array}{l} ∠B=∠C,\\ ∠D=∠EAC,\\ DA=AE,\end{array}\right. $所以$△DBA\cong △ACE$(AAS)。
[应用]设$∠EAC = ∠D = x^{\circ }$。因为$∠DAE = 70^{\circ }$，所以$∠DAC = ∠DAE + ∠EAC = (70 + x)^{\circ }$。因为$∠C = 110^{\circ }$，所以$∠E = \left180^{\circ } - ∠C - ∠EAC = (70 - x)^{\circ }\right$。因为$∠DAC = 3∠E$，所以$70 + x = 3(70 - x)$，解得$x = 35$，即$∠D = 35^{\circ }$。故当$∠D = 35^{\circ }$时，$∠DAC$的度数是$∠E$的3倍。

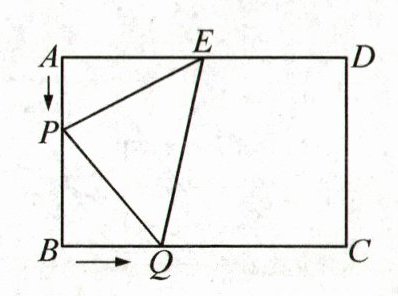
27. (8分)(2025·江苏无锡期末)如图,在长方形ABCD中,$AD= 6cm,AB= 4cm$,E为AD的中点.点P在线段AB上以1 cm/s的速度由点A向点B运动,到点B时停止;同时点Q在线段BC上由点B向点C运动,到点C时停止.
(1) 若点Q与点P的速度相同,则经过1s后,$△AEP与△BPQ$是否全等? 请说明理由,并判断此时线段PE和PQ之间的位置关系;
(2) 若点Q与点P的速度相同,设运动的时间为t s,$△PEQ的面积为S cm^{2}$,请用含t的代数式表示S;
(3) 若点Q与点P的速度不相同,则当点Q的速度为多少时,能够使$△AEP与△BPQ$全等?

答案：
(1)$△AEP\cong △BPQ$，PE⊥PQ。理由如下:因为四边形ABCD是长方形，所以$∠A = ∠B = 90^{\circ }$。因为E为AD的中点，AD = 6cm，所以$AE=\frac {1}{2}AD = 3cm$。因为点Q与点P的速度相同，所以BQ = AP = 1cm。因为AB = 4cm，所以BP = AB - AP = 3cm，所以AE = BP。在△AEP和△BPQ中，$\left\{\begin{array}{l} AP=BQ,\\ ∠A=∠B,\\ AE=BP,\end{array}\right. $所以$△AEP\cong △BPQ$(SAS)，所以$∠AEP = ∠BPQ$。因为$∠AEP + ∠APE = 90^{\circ }$，所以$∠BPQ + ∠APE = 90^{\circ }$，所以$∠EPQ = 180^{\circ } - (∠BPQ + ∠APE)=90^{\circ }$，所以PE⊥PQ。
(2)因为$4÷1 = 4(s)$，$6÷1 = 6(s)$，所以点P运动4s时停止，点Q运动6s时停止。分类讨论如下:①当$0≤t＜4$时，因为AE = 3cm，AP = tcm，$∠A = 90^{\circ }$，所以$S_{△APE}=\frac {1}{2}AP\cdot AE=\frac {3}{2}tcm^{2}$。因为AB = 4cm，所以BP = AB - AP = (4 - t)cm。因为BQ = tcm，$∠B = 90^{\circ }$，所以$S_{△BPQ}=\frac {1}{2}BP\cdot BQ=(-\frac {1}{2}t^{2}+2t)cm^{2}$。因为$S_{梯形ABQE}=\frac {1}{2}(AE + BQ)\cdot AB=(2t + 6)cm^{2}$，所以$S_{△PEQ}=S_{梯形ABQE}-S_{△APE}-S_{△BPQ}=(\frac {1}{2}t^{2}-\frac {3}{2}t + 6)cm^{2}$，即$S=\frac {1}{2}t^{2}-\frac {3}{2}t + 6$；②当$4≤t≤6$时，点P与点B重合，PQ = BQ = tcm，所以$S_{△PEQ}=\frac {1}{2}PQ\cdot AB = 2tcm^{2}$，即S = 2t。综上所述，$S=\left\{\begin{array}{l} \frac {1}{2}t^{2}-\frac {3}{2}t + 6(0≤t＜4),\\ 2t(4≤t≤6).\end{array}\right. $
(3)因为$v_{P}≠v_{Q}$，所以AP≠BQ，所以若△AEP与△BPQ全等，则只能是$△AEP\cong △BQP$，所以AP = BP且AE = BQ。设点Q的速度为xcm/s，运动的时间为ys，则$\left\{\begin{array}{l} y=4-y,\\ 3=xy,\end{array}\right. $解得$\left\{\begin{array}{l} x=\frac {3}{2},\\ y=2,\end{array}\right. $所以当点Q的速度为$\frac {3}{2}cm/s$时，能够使$△AEP$与$△BPQ$全等。