《2025年星推荐涂教材八年级数学下册人教版》

例5（厦门质检）如图，△ACE是以菱形ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称.若点B的坐标是(2，0)，则点E的坐标是_______.

答案： (4，-2√3)

例6 某数学兴趣小组在某数学课外活动中，研究三角形和正方形的性质时，做了如下探究：
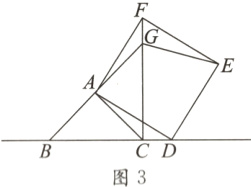
在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点(点D不与B，C重合)，以AD为边在AD右侧作正方形ADEF，连接CF.
(1)观察猜想
如图1，当点D在线段BC上时，
①BC与CF的位置关系为_______；
②BC，CD，CF之间的数量关系为_______.(将结论直接写在横线上)
(2)数学思考
如图2，当点D在线段CB的延长线上时，①②的结论是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明.
(3)拓展延伸
如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE.若已知AB=2√2，CD=1/4BC，请求出GE的长.
　　　
　　　　

答案：
$(1)①BC⊥CF；$$②BC=CD+CF$　　
$(2)$解：$①$的结论仍然成立，$②$的结论不成立，正确的结论是$BC=CD - CF.$证明如下：
∵四边形$ADEF$为正方形，
∴$AD=AF，$$∠DAF=90°.$
∵$∠BAC=90°，$
∴$∠DAB=∠FAC.$在$△DAB$和$△FAC$中，${AD=AF，∠DAB=∠FAC，AB=AC，}$
∴$△DAB≌△FAC(SAS).$
∴$DB=FC，$$∠DBA=∠FCA.$
∵$∠BAC=90°，$$AB=AC，$
∴$∠ABC=∠ACB=45°.$
∴$∠DBA=180° - ∠ABC=180° - 45°=135°.$
∴$∠FCA=∠DBA=135°.$
∴$∠BCF=∠FCA - ∠ACB=90°.$
∴$BC⊥CF.$
∵$BC=CD - DB，$$DB=CF，$
∴$BC=CD - CF.$　　
$(3)$如图，过点$A$作$A M \perp B C$于点$M，$过点$E$作$E N \perp B C ，$交$BC$的延长线于点$N，$过点$E$作$E P \perp CF$于点$P.$　　

由已知可证明$BC⊥CF，$得矩形$PCNE，$
∴$PE=CN.$
∵$∠BAC=90°，$$AB=AC=2√2，$
∴$BC=√(AB²+AC²)=4，$$AM=BM=MC=1/2BC=2.$
∵$CD=1/4BC，$
∴$CD=1，$$MD=MC+CD=3.$
∵$∠ADM+∠EDN=90°，$$∠EDN+∠DEN=90°，$
∴$∠ADM=∠DEN.$又
∵$∠AMD=∠DNE=90°，$$AD=DE，$
∴$△AMD≌△DNE(AAS).$
∴$DN=AM=2，$$NE=MD=3.$
∴$PE=CN=CD+DN=3，$$CP=NE=3.$
∵$∠BCG=90°，$$∠ABC=(180° - ∠BAC)/2=45°，$
∴$△BCG$为等腰直角三角形$.$
∴$CG=BC=4.$
∴$PG=CG - CP=4 - 3=1.$在$Rt△GPE$中，由勾股定理，得$GE=√(PG²+PE²)=√(1²+3²)=√10.$