《2025年课堂作业武汉出版社九年级数学下册人教版》

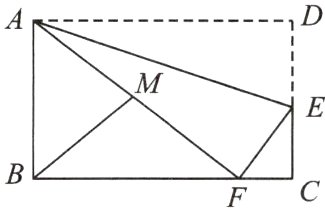
10. 如图，在矩形ABCD中，AD = 10，CD = 6，E是CD边上一点，沿AE折叠△ADE，使点D恰好落在BC边上的点F处。M是AF的中点，连接BM，则sin∠ABM = ________。

答案： $\frac{4}{5}$

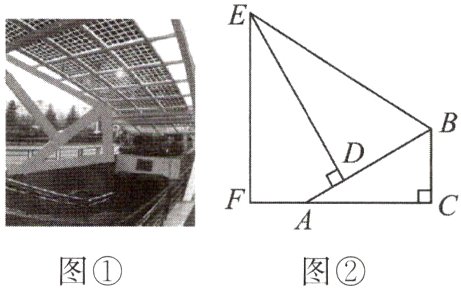
11. 图①是某地下商业街的入口，某数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF，如图②。经测量，支架的立柱BC与地面垂直，即∠BCA = 90°，且BC = 1.5 m，点F，A，C在同一条水平线上，斜杆AB与水平线AC的夹角∠BAC = 30°，支撑杆DE⊥AB于点D，该支架的边BE与AB的夹角∠EBD = 60°，又测得AD = 1 m，请你求出该支架的边BE的长度及顶端E到地面的距离EF。

答案： 过点B作BH⊥EF于点H.
∴四边形BCFH为矩形，
BC=HF=1.5，∠HBA=∠BAC=30°.
在Rt△ABC中，∠BAC=30°，BC=1.5，
∴AB=3.
∵AD=1，
∴BD=2.
在Rt△EDB中，
∵∠EBD=60°，
∴∠BED=90° - 60°=30°.
∴BE=2BD=2×2=4(m).
又
∵∠HBA=∠BAC=30°，
∴∠EBH=∠EBD - ∠HBD=30°.
∴EH=$\frac{1}{2}$BE=2.
∴EF=EH+HF=2+1.5=3.5(m).
故该支架的边BE的长度为4 m，顶端E到地面的距离EF为3.5 m.

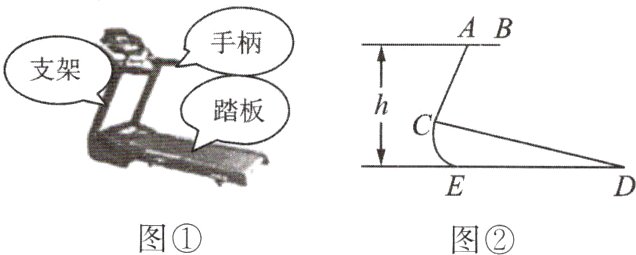
12. 图①和图②分别是某种型号跑步机的实物图与示意图。已知踏板CD长为1.6 m，CD与地面DE的夹角∠CDE为12°，支架AC长为0.8 m，∠ACD为80°，求跑步机手柄的一端A的高度h。（结果精确到0.1 m，参考数据：sin 12° = cos 78°≈0.21，sin 68° = cos 22°≈0.93，tan 68°≈2.48。）

答案： 过点C作CF⊥AB于点F，交DE于点G.
∵CD与地面DE的夹角∠CDE为12°，∠ACD=80°，
∴∠ACF=∠FCD - ∠ACD=90°+12° - 80°=22°.
∴∠CAF=68°.
在Rt△ACF中，
CF=AC·sin∠CAF=0.8×sin68°≈0.744.
在Rt△CDG中，
CG=CD·sin∠CDE=1.6×sin12°≈0.336.
∴h=FG=FC+CG≈0.744+0.336≈1.1(m).
故跑步机手柄的一端A的高度h约为1.1 m.