《2025年课堂作业武汉出版社九年级数学下册人教版》

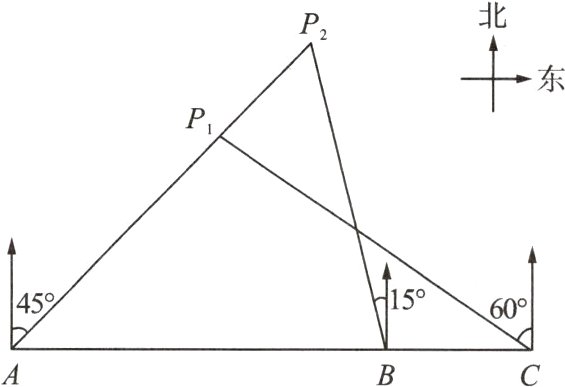
10.“国庆黄金周”期间，因东坡文化远近闻名的遗爱湖公园，游人络绎不绝，现有一艘游船载着游客在遗爱湖中游览.如图，当游船在A处时，船上游客发现岸上P1处的临皋亭和P2处的遗爱亭都在东北方向；当游船向正东方向行驶600 m到达B处时，游客发现遗爱亭在北偏西15°方向；当游船继续向正东方向行驶400 m到达C处时，游客发现临皋亭在北偏西60°方向.
　　(1)求A处到临皋亭P1处的距离.
　　(2)求临皋亭P1处与遗爱亭P2处之间的距离.(计算结果保留根号).
　　

答案： 10.
(1)在△AP₁C中，∠P₁AC = 45°，∠P₁CA = 30°.过点P₁作P₁N⊥AC于点N.设P₁N = x，则
AN = x，CN = $\sqrt{3}$x.又
∵AN + CN = AC = AB + BC，
∴x + $\sqrt{3}$x = 1000.
∴x = 500$\sqrt{3}$ - 500.
∴AP₁ = $\sqrt{2}$x = (500$\sqrt{6}$ - 500$\sqrt{2}$)(m).
(2)在△ABP₂中，∠ABP₂ = 75°，
∴∠AP₂B = 60°.过点B作BM⊥AP₂于点M，则AM = BM = 300$\sqrt{2}$.
∴MP₂ = $\frac{BM}{tan∠AP₂B}$ = 100$\sqrt{6}$.
∴AP₂ = AM + MP₂ = 300$\sqrt{2}$ + 100$\sqrt{6}$.
∴P₁P₂ = AP₂ - AP₁ = (800$\sqrt{2}$ - 400$\sqrt{6}$)(m).

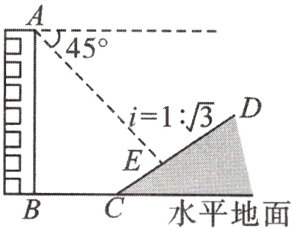
11.如图，楼房AB后有一假山，其坡度为$i = 1:\sqrt{3}$，山坡坡面上E点处有一休息亭.测得假山坡脚C与楼房水平距离BC = 25 m，与亭子距离CE = 20 m，从楼房顶测得E点的俯角为45°，求楼房AB的高.(注：坡度i是指坡面的铅直高度与水平宽度的比.)
　　

答案： 11.过点E分别作EF⊥BC交BC的延长线于点F，作EH⊥AB于点H.在Rt△CEF中，
∵i = $\frac{EF}{CF}$ = $\frac{1}{\sqrt{3}}$ = tan∠ECF，
∴∠ECF = 30°，EF = $\frac{1}{2}$CE = 10，
　CF = 10$\sqrt{3}$；BH = EF = 10.
∴HE = BF = BC + CF = 25 + 10$\sqrt{3}$.
　在Rt△AHE中，
∵∠HAE = 45°，
∴AH = HE = 25 + 10$\sqrt{3}$
∴AB = AH + HB = (35 + 10$\sqrt{3}$)(m).