《2025年长江全能学案同步练习册八年级数学上册人教版》

例1 计算：

(1) $ 3ab^{2} · (-\frac{1}{3}a^{2}b) · 2abc $；
(2) $ (-2x^{n - 1}y^{n}) · (-3xy) · (-\frac{1}{2}x^{2}z) $；
(3) $ -6m^{2}n · (x - y)^{3} · \frac{1}{3}mn^{2} · (y - x)^{2} $。

答案：
(1)
$3ab^{2}·(-\frac{1}{3}a^{2}b)·2abc$
$=[3×(-\frac{1}{3})×2]·(a· a^{2}· a)·(b^{2}· b· b)· c$
$=-2a^{1 + 2+1}b^{2 + 1+1}c$
$=-2a^{4}b^{4}c$
(2)
$(-2x^{n - 1}y^{n})·(-3xy)·(-\frac{1}{2}x^{2}z)$
$=[(-2)×(-3)×(-\frac{1}{2})]·(x^{n - 1}· x· x^{2})·(y^{n}· y)· z$
$=-3x^{n - 1+1 + 2}y^{n + 1}z$
$=-3x^{n + 2}y^{n + 1}z$
(3)
因为$(y - x)^{2}=(x - y)^{2}$，
所以$-6m^{2}n·(x - y)^{3}·\frac{1}{3}mn^{2}·(y - x)^{2}$
$=[(-6)×\frac{1}{3}]·(m^{2}· m)·(n· n^{2})·(x - y)^{3}·(x - y)^{2}$
$=-2m^{3}n^{3}(x - y)^{3 + 2}$
$=-2m^{3}n^{3}(x - y)^{5}$

例2 计算：
(1) $ (0.3x^{3}y^{4})^{2} · (-0.2x^{4}y^{3})^{2} $；
(2) $ 5a^{3}b · (-3b)^{2} + (-6ab)^{2} · (-ab) - ab^{3} · (-4a)^{2} $；
(3) $ -4(-a^{2}bc)^{2} · 3a · (bc)^{3} - (-abc)^{3} · (-abc)^{2} $。

答案：
(1) 原式$=(0.3^2x^{3×2}y^{4×2})·((-0.2)^2x^{4×2}y^{3×2})$
$=(0.09x^6y^8)·(0.04x^8y^6)$
$=0.09×0.04x^{6+8}y^{8+6}$
$=0.0036x^{14}y^{14}$
(2) 原式$=5a^3b·9b^2+36a^2b^2·(-ab)-ab^3·16a^2$
$=45a^3b^3-36a^3b^3-16a^3b^3$
$=(45-36-16)a^3b^3$
$=-7a^3b^3$
(3) 原式$=-4(a^4b^2c^2)·3a·(b^3c^3)-(-a^3b^3c^3)·(a^2b^2c^2)$
$=-12a^5b^5c^5-(-a^5b^5c^5)$
$=-12a^5b^5c^5+a^5b^5c^5$
$=-11a^5b^5c^5$

例3 纳米是一种长度单位,1米等于$ 10^{9} $纳米,试计算长为5米、宽为4米、高为3米的长方体的体积是多少立方纳米。

答案： 5米=$5×10^{9}$纳米，4米=$4×10^{9}$纳米，3米=$3×10^{9}$纳米。
$V=(5×10^{9})×(4×10^{9})×(3×10^{9})$
$=(5×4×3)×(10^{9}×10^{9}×10^{9})$
$=60×10^{27}$
$=6×10^{28}$(立方纳米)
故长为5米、宽为4米、高为3米的长方体的体积是$6×10^{28}$立方纳米。

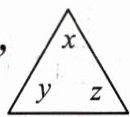
(1)“三角”表示$ 3xyz $,“方框”表示$ -4a^{b}d^{c} $,则×= -36m⁶n³。


(2)若$ 1 + 2 + 3 + … + n = m $,则$ (ab^{n}) \cdot (a^{2}b^{n - 1})…(a^{n - 1}b^{2}) \cdot (a^{n}b) = $(ab)ᵐ。

答案：
(1)-36m⁶n³；
(2)(ab)ᵐ