《2025年智慧学习明天出版社八年级数学上册人教版》

21. (6 分)证明：如果两个三角形有两条边和其中一边上的中线分别相等,那么这两个三角形全等.

答案： 已知：在△ABC和△DEF中，AB=DE，AC=DF，AD是△ABC的边BC上的中线，DG是△DEF的边EF上的中线，且AD=DG。
证明：延长AD至点M，使DM=AD，连接BM；延长DG至点N，使NG=DG，连接EN。
∵AD是BC边上的中线，
∴BD=CD。
在△ADC和△MDB中，
AD=MD，
∠ADC=∠MDB，
CD=BD，
∴△ADC≌△MDB(SAS)。
∴AC=MB。
同理可证△DGF≌△NGE(SAS)，
∴DF=NE。
∵AC=DF，
∴MB=NE。
∵AD=DG，
∴AM=2AD=2DG=DN。
在△ABM和△DEN中，
AB=DE，
BM=EN，
AM=DN，
∴△ABM≌△DEN(SSS)。
∴∠BAD=∠EDN。
在△ABD和△DEG中，
AB=DE，
∠BAD=∠EDG，
AD=DG，
∴△ABD≌△DEG(SAS)。
∴BD=EG。
∴BC=2BD=2EG=EF。
在△ABC和△DEF中，
AB=DE，
AC=DF，
BC=EF，
∴△ABC≌△DEF(SSS)。

22. (6 分)如图,点 $ E $,$ C $ 在线段 $ BF $ 上,$ BE = CF $. 有下面四个等式：①$ AB = DE $,②$ \angle ACB = \angle F $,③$ \angle A = \angle D $,④$ AC = DF $. 请选出

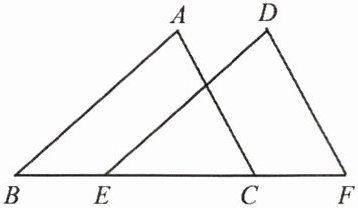
两

个

作为条件,推出 $ \triangle ABC \cong \triangle DEF $,并予以证明.(写出一种情况即可)
已知：①,④.
求证：$ \triangle ABC \cong \triangle DEF $.

证明:∵BE=CF,∴BE+EC=CF+EC,即BC=EF.在△ABC和△DEF中,AB=DE,BC=EF,AC=DF,∴△ABC≌△DEF(SSS).

答案： ①;④ 证明:
∵BE=DF,
∴BE+EC=CF+EC,即BC=EF.在△ABC和△DEF中,AB=DE,BC=EF,AC=DF,
∴△ABC≌△DEF.

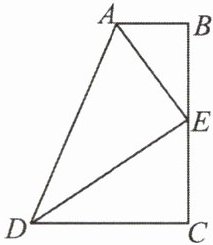
23. (7 分)如图,在四边形 $ ABCD $ 中,$ \angle B = \angle C = 90° $,点 $ E $ 为 $ BC $ 的中点,且 $ DE $ 平分 $ \angle ADC $. 求证：
(1)$ AE $ 平分 $ \angle BAD $；
(2)$ AB + CD = AD $.

答案：

(1)提示:过点E作EF⊥AD于F.
(2)
∵AE平分∠BAD,DE平分∠ADC,EF⊥AD,∠B=∠C=90°,
∴AB=AF,DC=DF.
∴AB+CD=AF+FD=AD.

24. (8 分)如图,在四边形 $ ABCD $ 中,$ BC ＞ DA $,$ AD = DC $,$ BD $ 平分 $ \angle ABC $,$ DH \perp BC $ 于 $ H $. 求证：
(1)$ \angle DAB + \angle C = 180° $；
(2)$ BH = \frac{1}{2}(AB + BC) $.

答案：

(1)过D作DE⊥AB,交BA延长线于E.
∵BD平分∠ABC,DH⊥BC,
∴DH=DE.在Rt△ADE和Rt△CDH中，$\left\{\begin{array}{l} DH=DE,\\ AD=DC,\end{array}\right. $
∴Rt△ADE≌Rt△CDH(HL).
∴∠C=∠DAE.
∵∠DAB+∠DAE=180°,
∴∠DAB+∠C=180°.
(2)在Rt△BDE和Rt△BDH中，$\left\{\begin{array}{l} DE=DH,\\ BD=BD,\end{array}\right. $
∴Rt△BDE≌Rt△BDH(HL).
∴BE=BH.
∵Rt△ADE≌Rt△CDH,
∴AE=CH.
∴AB+BC=AB+BH+CH=BE+BH=2BH.
∴BH=$\frac {1}{2}$(AB+BC).