《2025年经纶学典5星学霸七年级数学上册苏科版》

1. 点 $ A $ 在数轴上所表示的数如图所示,将点 $ A $ 向左平移 $ 2 $ 个单位长度,得到点 $ B $ 的相反数,点 $ P $ 是数轴上一动点.

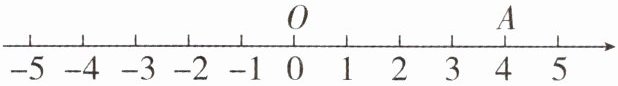
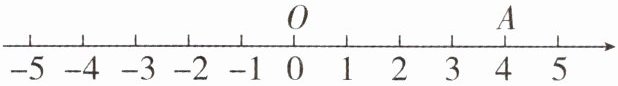
(1) 点 $ B $ 表示的数是-2.
(2) 若点 $ B $ 在数轴上移动了 $ m $ 个单位长度得到点 $ C $,且 $ AC = 3 $,求 $ m $ 的值.
因为点 A 表示的数是 4,AC=3,设点 C 表示的数为 $x_C$,所以 $|4-x_C|=3$,所以 $4-x_C=3$ 或 $4-x_C=-3$,解得 $x_C=1$ 或 $x_C=7$,因为点 B 表示的是-2,所以需向右平移 $1-(-2)=3$(个)单位长度或 $7-(-2)=9$(个)单位长度,故 $m=3$ 或 $m=9$.
(3) 若点 $ D $ 为 $ AP $ 的中点,点 $ E $ 为 $ BP $ 的中点,点 $ P $ 在运动过程中,线段 $ DE $ 的长度是否发生变化? 若不发生变化,请你求出线段 $ DE $ 的长度;若发生变化,请你说明理由.
不变.设点 P 表示的数是 $x_P$,点 D 表示的数是 $x_D$,点 E 表示的数是 $x_E$,因为点 B 表示的数是-2,点 A 表示的数是 4,当 $x_P＜-2$ 时,$x_D=\frac{4+x_P}{2}$,$x_E=\frac{-2+x_P}{2}$,所以 $DE=x_D-x_E=\frac{4+x_P}{2}-\frac{-2+x_P}{2}=3$;当 $-2\leqslant x_P\leqslant 4$ 时,$x_D=\frac{4+x_P}{2}$,$x_E=\frac{-2+x_P}{2}$,所以 $DE=x_D-x_E=\frac{4+x_P}{2}-\frac{-2+x_P}{2}=3$;当 $x_P＞4$ 时,$x_D=\frac{4+x_P}{2}$,$x_E=\frac{-2+x_P}{2}$,所以 $DE=x_D-x_E=\frac{4+x_P}{2}-\frac{-2+x_P}{2}=3$.故线段 DE 的长度不变,为 3.

答案： 1.
(1)-2
(2)因为点 A 表示的数是 4,AC=3,设点 C 表示的数为 $x_C$,所以 $|4-x_C|=3$,所以 $4-x_C=3$ 或 $4-x_C=-3$,解得 $x_C=1$ 或 $x_C=7$,因为点 B 表示的是-2,所以需向右平移 $1-(-2)=3$(个)单位长度或 $7-(-2)=9$(个)单位长度,故 $m=3$ 或 $m=9$.
(3)不变.设点 P 表示的数是 $x_P$,点 D 表示的数是 $x_D$,点 E 表示的数是 $x_E$,因为点 B 表示的数是-2,点 A 表示的数是 4,当 $x_P＜-2$ 时,$x_D=\frac{4+x_P}{2}$,$x_E=\frac{-2+x_P}{2}$,所以 $DE=x_D-x_E=\frac{4+x_P}{2}-\frac{-2+x_P}{2}=3$;当 $-2\leqslant x_P\leqslant 4$ 时,$x_D=\frac{4+x_P}{2}$,$x_E=\frac{-2+x_P}{2}$,所以 $DE=x_D-x_E=\frac{4+x_P}{2}-\frac{-2+x_P}{2}=3$;当 $x_P＞4$ 时,$x_D=\frac{4+x_P}{2}$,$x_E=\frac{-2+x_P}{2}$,所以 $DE=x_D-x_E=\frac{4+x_P}{2}-\frac{-2+x_P}{2}=3$.故线段 DE 的长度不变,为 3.

2. (2024·六安期末) 数轴上表示 $ 5 $ 和 $ 2 $ 的两点之间的距离是 $ |5 - 2| = 3 $;表示 $ -3 $ 和 $ 2 $ 的两点之间的距离是 $ |-3 - 2| = 5 $;一般地,数轴上表示数 $ m $ 和数 $ n $ 的两点之间的距离等于 $ |m - n| $.
(1) 如果表示数 $ a $ 和 $ -2 $ 的两点之间的距离是 $ 3 $,那么可列方程为 $ |a - (-2)| = 3 $,则 $ a = $1 或-5;
(2) 若数轴上表示数 $ a $ 的点位于表示 $ -4 $ 与 $ 2 $ 的两点之间,则 $ |a + 4| + |a - 2| = $6;
(3) 如果点 $ A $ 表示 $ -8 $、点 $ B $ 表示 $ -4 $、点 $ C $ 表示 $ 2 $,点 $ P $ 从点 $ A $ 出发,以每秒 $ 2 $ 个单位长度的速度沿数轴向右运动,运动时间为 $ t $ 秒,在一段时间内 $ PB + PC $ 的值不变,直接写出 $ t $ 的取值范围.
t 的取值范围是 $2\leqslant t\leqslant 5$.

答案： 2.
(1)1 或-5
(2)6
(3)t 的取值范围是 $2\leqslant t\leqslant 5$. 解析:根据题意可知,当点 P 在线段 BC 上运动时,$PB+PC$ 的值不变,点 P 从点 A 运动到点 B 的时间为 $t=|-4-(-8)|÷2=2$(秒),点 P 从点 A 运动到点 C 的时间为 $t=|2-(-8)|÷2=5$(秒),所以当 $2\leqslant t\leqslant 5$ 时,$PB+PC$ 的值不变.