《2025年经纶学典5星学霸七年级数学上册苏科版》

1. (2025·宿迁期末)如图,将一张长方形纸片分别沿着 EP,FP 对折,使点 B 落在点 $ B' $,点 C 落在点 $ C' $,点 $ P,B',C' $不在同一直线上,若 $ ∠EPF+∠B'PC'= 111^{\circ} $,则 $ ∠B'PC' $的度数为 (D)
A.$ 10^{\circ} $
B.$ 8^{\circ} $
C.$ 12^{\circ} $
D.$ 14^{\circ} $

答案： D

2. (2025·泰州期末)如图,将长方形纸片 ABCD 的一角折叠,使顶点 A 落在点 $ A' $处,折痕为 EO.点 F 为射线 BC 上一点,连接 OF,将长方形纸片的另一角 $ ∠B $沿 OF 折叠,使得点 B 落在点 $ B' $处(折痕为 OF).若 $ ∠A'OB'= 36^{\circ} $,则 $ ∠EOF= $______ $ ^{\circ} $.

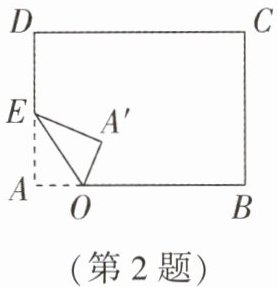
答案：
108或72　　解析:由题意可知,∠AOE=∠A'OE=$\frac{1}{2}$∠AOA',∠BOF+∠B'OF=$\frac{1}{2}$∠BOB',所以∠AOA'=2∠AOE,∠BOB'=2∠BOF。
①当OB'在∠AOA'的外部时,如图①,因为∠AOA'+∠BOB'+∠A'OB'=180°,且∠A'OB'=36°,2∠AOE+2∠BOF+∠A'OB'=180°,所以∠AOE+∠BOF=$\frac{180° - ∠A'OB'}{2}$=$\frac{180° - 36°}{2}$=72°,所以∠EOF=180°−(∠AOE+∠BOF)=180°−72°=108°;
　　　 　　
②当OB'在∠AOA'的内部时,如图②,因为∠AOA'+∠BOB'−∠A'OB'=180°,且∠A'OB'=36°,所以2∠AOE+2∠BOF−∠A'OB'=180°,所以∠AOE+∠BOF=$\frac{180° + ∠A'OB'}{2}$=$\frac{180° + 36°}{2}$=108°,所以∠EOF=180°−(∠AOE+∠BOF)=180°−108°=72°。
综上,∠EOF=108°或72°。

3. (2024·南京期末)已知 $ ∠AOB= 90^{\circ} $,以 O 为端点画射线 OM.将射线 OM 沿直线 OA 翻折,得到射线 ON,将射线 OM 绕点 O 顺时针旋转 $ 60^{\circ} $,得到射线 OP.若 $ ∠NOP= 10^{\circ} $,则 $ ∠BOM= $______ $ ^{\circ} $.

答案：
55或65或115或125　解析:
①当ON,OP在∠AOB的内部,ON在OP上方时,如图①,因为∠MOP=60°,∠NOP=10°,所以∠MON=50°。由翻折得,∠AOM=$\frac{1}{2}$∠MON=25°,所以∠BOM=∠AOM+∠AOB=115°;
　　　
②当ON,OP在∠AOB的内部,ON在OP下方时,如图②,因为∠MOP=60°,∠NOP=10°,所以∠MON=70°。由翻折得,∠AOM=$\frac{1}{2}$∠MON=35°,所以∠BOM=∠AOM+∠AOB=125°;
③当ON,OP在∠AOB的外部,ON在OP下方时,如图③,因为∠MOP=60°,∠NOP=10°,所以∠MON=50°。由翻折得,∠FOM=$\frac{1}{2}$∠MON=25°,所以∠BOM=∠BOF−∠FOM=65°;
　　
④当ON,OP在∠AOB的外部,ON在OP上方时,如图④,因为∠MOP=60°,∠NOP=10°,所以∠MON=70°。由翻折得,∠FOM=$\frac{1}{2}$∠MON=35°,所以∠BOM=∠BOF−∠FOM=55°。
综上,∠BOM=55°或65°或115°或125°。

4. 问题情境:
数学活动课上,如图①,老师拿一张长方形纸片折叠一角,得到折痕 EF,同学们发现折痕有角平分线的作用.
问题解决:
(1)若 $ ∠EFA'= 35^{\circ} $,则 $ ∠A'FB= $______110°;
(2)实践探究:希望小组受此问题的启发,将长方形纸片按图②方式折叠,EF,FG 为折痕,点 $ A' $, $ B' $,F 恰好在同一条直线上,求 $ ∠EFG $的度数;
根据题意,得∠A'FE=∠AFE=$\frac{1}{2}$∠A'FA,∠B'FG=∠GFB=$\frac{1}{2}$∠B'FB,所以∠EFG=∠A'FE+∠B'FG=$\frac{1}{2}$(∠A'FA+∠B'FB)=$\frac{1}{2}$×180°=90°。
(3)拓展延伸:智慧小组将长方形纸片按图③方式折叠,DE,CE 为折痕,若 $ ∠A'EB'= 15^{\circ} $,请直接写出 $ ∠DEC $的度数.
82.5°

答案：
(1)110°　　解析:因为折痕FE是∠AFA'的平分线,∠EFA'=35°,所以∠AFE=35°。因为∠A'FB=180°−∠AFE−∠A'FE,所以∠A'FB=180°−35°−35°=110°。
(2)根据题意,得∠A'FE=∠AFE=$\frac{1}{2}$∠A'FA,∠B'FG=∠GFB=$\frac{1}{2}$∠B'FB,所以∠EFG=∠A'FE+∠B'FG=$\frac{1}{2}$(∠A'FA+∠B'FB)=$\frac{1}{2}$×180°=90°。
(3)∠DEC=82.5°。　　解析:根据题意,得∠AED=∠DEA',∠BEC=∠CEB'。因为∠DEC=∠CEB'+∠DEA'−∠A'EB',且∠A'EB'=15°,所以∠AED+∠DEA'+∠CEB'+∠BEC=180°+15°=195°,所以∠AED+∠BEC=$\frac{1}{2}$×195°=97.5°,所以∠DEC=180°−97.5°=82.5°。