《2025年经纶学典5星学霸七年级数学上册苏科版》

2. (2025·宿迁期末)(1)如图①,$\angle EFG= 120^{\circ}$,顶点$F在直线CD$上,边$FE$,$FG分别与直线AB交于点M$,$H$,且$\angle CFE+\angle GHB= 60^{\circ}$。试说明$AB// CD$；
(2)如图②,在(1)的条件下分别作$\angle EFD与\angle AHG的平分线FN$,$HN交于点N$,求$\angle N$的度数；
(3)如图③,在(1)的条件下作$\angle CFE的平分线FI$,过点$H作一条射线HQ$,交直线$FI于点P$,当$\angle HPF= 30^{\circ}$时,请直接写出$\angle BHP与\angle FHP$的关系式。

答案：
2.
(1)因为∠EFG=120°,顶点F在直线CD上,所以∠CFE+∠GFD=180° - ∠EFG=180° - 120°=60°.因为∠CFE+∠GHB=60°,所以∠GHB=∠GFD,所以AB//CD.
(2)如图①,作NK//AB,易证NK//CD,所以∠AHN=∠HNK,∠CFN=∠FNK,所以∠FNH=∠FNK - ∠HNK=∠CFN - ∠AHN.设∠GFD=α,所以∠CFE=60° - α,∠GHB=α,∠AHG=180° - α.因为∠EFG=120°,所以∠EFD=120°+α.因为FN是∠EFD的平分线,所以∠EFN= $\frac{1}{2}(120°+α)=60°+\frac{1}{2}α$,所以∠CFN=∠EFN+∠CFE=$(60°+\frac{1}{2}α)+(60° - α)=120°-\frac{1}{2}α$.因为HN是∠AHG的平分线,所以∠AHN=$\frac{1}{2}∠AHG=\frac{1}{2}(180° - α)=90°-\frac{1}{2}α$,所以∠FNH=∠CFN - ∠AHN=$(120°-\frac{1}{2}α)-(90°-\frac{1}{2}α)=30°$.
　　　　　　　
(3)∠BHP+∠FHP=180°或∠FHP - ∠BHP=60°. 解析:①当点P在CD的上方时,如图②,过点P作PT//AB.设∠IFC=β,因为FI平分∠CFE,所以∠EFI=∠CFI=β,则∠GFD=180° - ∠EFC - ∠EFG=60° - 2β.因为AB//CD,所以∠FHB=∠CFG=180° - ∠GFD=120°+2β.因为PT//AB,AB//CD,所以PT//CD,所以∠AHP=∠HPT,∠TPF=∠IFC=β.又因为∠HPF=30°,所以∠AHP=∠HPT=∠HPF - ∠FPT=∠HPF - ∠IFC=30° - β,所以∠BHP=180° - ∠AHP=180° - (30° - β)=150°+β,所以∠FHP=∠BHP - ∠FHB=(150°+β) - (120°+2β)=30° - β,所以∠BHP+∠FHP=(150°+β)+(30° - β)=180°,即∠BHP+∠FHP=180°;
　　 　　
②当点P在CD的下方时,如图③,过点P作PT//CD,设∠IFC=β,所以∠DFP=∠CFI=β.因为PT//CD,所以∠FPT=∠DFP=β.因为AB//PT,所以∠BHP=∠HPT=∠HPF+∠FPT=30°+β.因为∠GFD=180° - ∠EFC - ∠EFG=60° - 2β,∠FHB=∠CFG=120°+2β,所以∠FHP=∠FHB - ∠BHP=(120°+2β) - (30°+β)=90°+β,所以∠FHP - ∠BHP=(90°+β) - (30°+β)=60°.综上所述,∠BHP+∠FHP=180°或∠FHP - ∠BHP=60°.

3. (2024·扬州期末)经过平行线中的拐点作平行线是解决与平行线有关问题的常用思路。
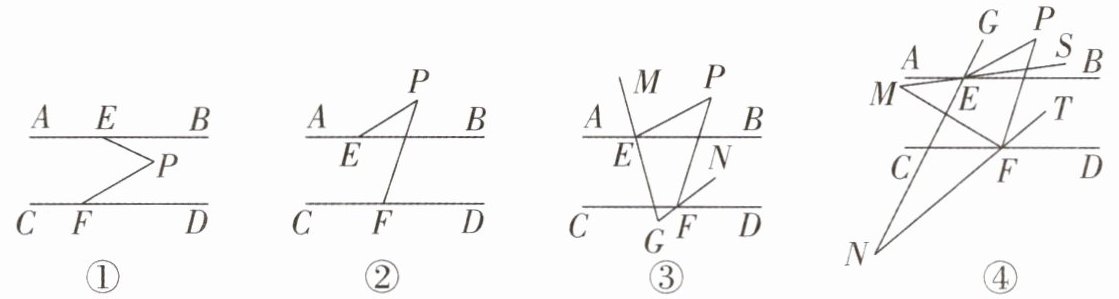
(1)如图①,$AB// CD$,$\angle BEP= 25^{\circ}$,$\angle PFC= 150^{\circ}$,则$\angle EPF= $____；
(2)如图②,$AB// CD$,点$P在直线AB$的上方($\angle AEP＞\angle CFP$),探究$\angle AEP$、$\angle CFP$、$\angle EPF$之间的数量关系,并说明理由；
(3)如图③,$AB// CD$,点$P在直线AB$上方,$\angle AEP的平分线EM所在的直线和\angle DFP的平分线FN所在的直线交于点G$(点$G在直线CD$的下方),请写出$\angle EPF和\angle EGF$之间的数量关系,并说明理由；
(4)如图④,$AB// CD$,点$P在直线AB$上方,$EG$,$ES$,$FM$,$FT分别是\angle AEP$、$\angle BEP$、$\angle CFP$、$\angle DFP$的三等分线,且$\frac{\angle AEG}{\angle AEP}= \frac{\angle PES}{\angle PEB}= \frac{\angle MFP}{\angle CFP}= \frac{\angle DFT}{\angle DFP}= \frac{2}{3}$。直线$ES与直线FM交于点M$,直线$EG与直线FT交于点N$(点$N在直线CD$的下方)。请直接写出$\angle EMF$、$\angle ENF与\angle P$之间的数量关系。

答案：
3.
(1)55°　解析:如图①,过点P作PH//AB,所以∠EPH=∠BEP=25°.因为AB//CD,所以PH//CD,所以∠FHP=180° - ∠PFC=30°,所以∠EPF=∠EPH+∠FHP=55°.
　　　　　　 　　
(2)∠EPF=∠AEP - ∠CFP,理由:如图②,过点P作PH//AB,所以∠EPH=180° - ∠AEP.因为AB//CD,所以PH//CD,∠FPH=180° - ∠CFP,∠EPF=∠FPH - ∠EPH=(180° - ∠CFP) - (180° - ∠AEP)=∠AEP - ∠CFP,所以∠EPF=∠AEP - ∠CFP.
(3)∠EPF+2∠EGF=180°,理由:因为EM平分∠AEP,FN平分∠DFP,所以∠AEM=∠PEM,∠PFN=∠DFN.设∠AEM=∠PEM=∠1,∠PFN=∠DFN=∠2,则∠AEP=2∠1,∠DFP=2∠2,∠CFP=180° - 2∠2,如图③,过点P作PH//AB,过点G作KL//AB,由
(2)可知,∠EPF=∠AEP - ∠CFP=2∠1 - (180° - 2∠2)=2(∠1+∠2) - 180°,因为KL//AB,所以∠KGE=∠AEM=∠1.因为AB//CD,所以KL//CD,所以∠LGN=∠DFN=∠2,∠EGF=180° - ∠KGE - ∠LGN=180° - (∠1+∠2).因为180° - 2[180° - (∠1+∠2)]=2(∠1+∠2) - 180°,所以180° - 2∠EGF=∠EPF,所以∠EPF+2∠EGF=180°.
　　　 　　
(4)∠EMF+∠ENF+∠P=120°.