《2025年经纶学典5星学霸七年级数学上册苏科版》

1. (2025·连云港期末)如图①纸片 $ABCD(AD// BC)$,将 $CD$ 按如图②所示沿着 $DE$ 折叠至 $DC'$, $DC'$ 与线段 $BC$ 交于点 $F$, $\angle BFD = m$,点 $E$ 在线段 $BC$ 上,若将 $AD$ 按如图③所示沿着 $DO$ 折叠至 $DA'$,且点 $A'$ 在线段 $DC$ 的延长线上,点 $O$ 在线段 $BC$ 上,则 $\angle ODE = $ $90^{\circ}-\frac{1}{2}m$.

答案： $90^{\circ}-\frac{1}{2}m$

2. (2024·泰州期中)如图,将长方形纸片 $ABCD$ 沿 $EF$ 折叠后,点 $C$, $D$ 分别落在点 $C'$, $D'$ 的位置, $C'D'$ 交 $BC$ 于点 $G$,再将 $\triangle C'FG$ 沿 $FG$ 折叠,点 $C'$ 落在点 $C''$ 的位置(点 $C''$ 在折痕 $EF$ 的左侧).
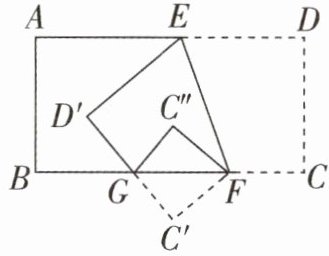
(1)如果 $\angle FED' = 65^{\circ}$,求 $\angle EFC$ 的度数；
(2)如果 $\angle AED' = 40^{\circ}$,则 $\angle EFC'' = $ ____30$^{\circ}$；
(3)探究 $\angle EFC''$ 与 $\angle AED'$ 的数量关系,并说明理由.

答案：
(1)根据题意,得$AD// BC$,所以$∠DEF+∠EFC=180^{\circ}$.因为折叠,且$∠FED'=65^{\circ}$,所以$∠DEF=∠D'EF=65^{\circ}$,所以$∠EFC=180^{\circ}-∠DEF=115^{\circ}$.
(2)30 解析:因为$∠AED'=40^{\circ}$,所以$∠DED'=180^{\circ}-∠AED'=140^{\circ}$,由
(1)知$∠DEF=∠D'EF$,所以$∠DEF=∠D'EF=\frac{1}{2}∠DED'=70^{\circ}$.因为$AD// BC$,所以$∠EFC=180^{\circ}-∠DEF=110^{\circ}$.因为折叠,所以$∠EFC'=∠EFC=110^{\circ}$.因为$∠EFC=110^{\circ}$,所以$∠EFG=180^{\circ}-∠EFC=70^{\circ}$,所以$∠C'FG=∠EFC'-∠EFG=40^{\circ}$.因为折叠,所以$∠C'FG=∠C''FG=40^{\circ}$,所以$∠EFC''=∠EFG-∠GFC''=30^{\circ}$.
(3)$∠EFC''+\frac{3}{2}∠AED'=90^{\circ}$,理由:设$∠AED'=\alpha$,所以$∠DED'=180^{\circ}-∠AED'=180^{\circ}-\alpha$.由
(1)知$∠DEF=∠D'EF$,所以$∠DEF=∠D'EF=\frac{1}{2}∠DED'=\frac{180^{\circ}-\alpha}{2}$.因为$AD// BC$,所以$∠EFC=180^{\circ}-∠DEF=90^{\circ}+\frac{1}{2}\alpha$.因为折叠,所以$∠EFC'=∠EFC=90^{\circ}+\frac{1}{2}\alpha$.因为$∠EFC=90^{\circ}+\frac{1}{2}\alpha$,所以$∠EFG=180^{\circ}-∠EFC=90^{\circ}-\frac{1}{2}\alpha$,$∠C'FG=∠EFC'-∠EFG=\alpha$.因为折叠,所以$∠C'FG=∠C''FG=\alpha$,所以$∠EFC''=∠EFG-∠GFC''=90^{\circ}-\frac{3}{2}\alpha$,$∠EFC''=90^{\circ}-\frac{3}{2}∠AED'$,所以$∠EFC''+\frac{3}{2}∠AED'=90^{\circ}$.

3. (2025·泰州月考)操作与探究：
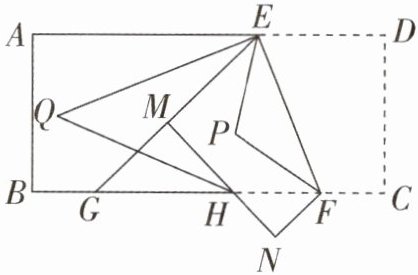
如图,已知长方形的每个内角都是直角,将一张长方形纸片 $ABCD$ 沿 $EF$ 折叠后,点 $D$, $C$ 的对应点分别是 $M$, $N$, $EM$ 的延长线与 $BC$ 相交于点 $G$, $MN$ 与 $BC$ 相交于点 $H$.
(1)若 $\angle EFG = 68^{\circ}$,求 $\angle EGF$ 的度数.
(2) $\angle AEM$ 与 $\angle BHM$ 的平分线相交于点 $Q$,求 $\angle Q$ 的度数.
(3)设 $\angle FEM$ 与 $\angle GFE$ 的平分线相交于点 $P$, $\angle EFG$ 与 $\angle P$ 之间存在某种关系,你能找出这个关系吗？说明理由.

答案：

(1)由题意得,$AD// BC$,$∠DEF=∠GEF$,所以$∠DEF=∠EFG=∠GEF$.因为$∠EFG=68^{\circ}$,所以$∠DEF=∠GEF=68^{\circ}$,$∠AEG=180^{\circ}-(68^{\circ}+68^{\circ})=44^{\circ}$,所以$∠EGF=∠AEG=44^{\circ}$.
(2)如图,过点 Q 作$QR// AD$,所以$QR// AD// BC$,$∠EQR=∠AEQ$,$∠HQR=∠QHB$,所以$∠EQH=∠AEQ+∠QHB$.同理可得,$∠EMH=∠AEM+∠MHB$.因为$∠AEM$与$∠BHM$的平分线相交于点 Q,所以$∠AEQ=\frac{1}{2}∠AEM$,$∠QHB=\frac{1}{2}∠MHB$,所以$∠EQH=\frac{1}{2}∠EMH=\frac{1}{2}×90^{\circ}=45^{\circ}$.

(3)$∠P=180^{\circ}-∠EFG$,理由如下:由
(2)得,$∠P=∠AEP+∠PFB$.因为$∠FEM$与$∠GFE$的平分线相交于点 P,所以$∠PEG=\frac{1}{2}∠GEF=\frac{1}{2}∠FED=\frac{1}{2}∠EFG$,$∠PFG=\frac{1}{2}∠EFG$.又因为$∠AEG=180^{\circ}-(∠FED+∠GEF)=180^{\circ}-2∠EFG$,所以$∠P=∠AEP+∠PFB=∠AEG+∠PEG+∠PFB=(180^{\circ}-2∠EFG)+\frac{1}{2}∠EFG+\frac{1}{2}∠EFG=180^{\circ}-∠EFG$.