《2026年全效学习中考学练测数学浙江专版》

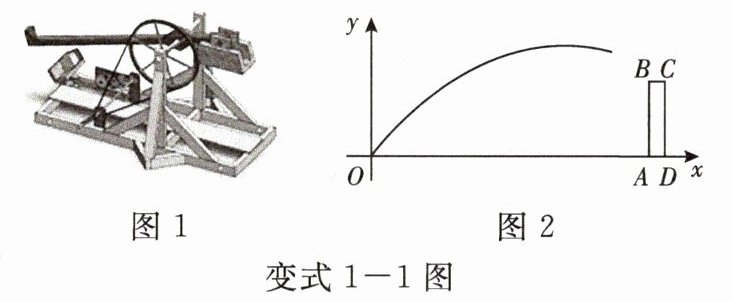
变式 1 - 1 [2025·衢州模拟]发石车（图 1）是古代一种攻城器械，据《三国志》记载：曹操创制发石车，攻破袁绍军壁楼. 如图 2，发石车位于点 $ O $ 处，其前方有一堵壁楼，其防御墙的竖直截面为矩形 $ ABCD $，墙宽 $ BC $ 为 2 米，点 $ A $ 与点 $ O $ 的水平距离为 28 米，墙高 $ AB $ 为 6 米. 以点 $ O $ 为原点，水平方向为 $ x $ 轴方向，建立直角坐标系，将石块视为一个点，其飞行路线近似为抛物线 $ y = a(x - 20)^2 + k $（$ a \neq 0 $）.
（1）若发射石块在空中飞行的最大高度为 10 米.
①求该抛物线的表达式.
②判断石块能否飞越防御墙，并说明理由.
（2）若要使石块恰好落在防御墙顶部 $ BC $ 上（包括点 $ B $，$ C $），求 $ a $ 的取值范围.

答案： 变式1-1
(1)$y=-\frac{1}{40}(x - 20)^{2}+10$ ②石块能飞跃防御墙.理由略
(2)$-\frac{1}{50}\leq a\leq-\frac{1}{56}$

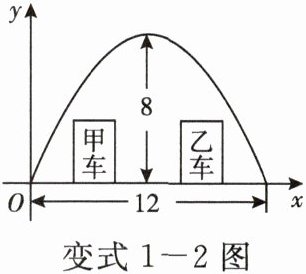
变式 1 - 2 [2025·新疆]天山胜利隧道预计于 2025 年建成通车，它将成为世界上最长的高速公路隧道，能大大提升区域交通效率，促进经济发展. 如图是隧道截面图，其轮廓可近似看作是抛物线的一部分. 若隧道底部宽 12 米，高 8 米，按照如图所示的方式建立平面直角坐标系.
（1）求抛物线的函数表达式.
（2）该隧道设计为单向双车道通行，车辆顶部在竖直方向上与隧道的空隙不少于 0.5 米，当两辆车在隧道内并排行驶时，需沿中心线两侧行驶，且两车至少间隔 2 米（中心线宽度不计）. 若宽 3 米，高 3.5 米的两辆车并排行驶，能否安全通过？请说明理由.
]

答案： 变式1-2
(1)$y=-\frac{2}{9}(x - 6)^{2}+8(0\leq x\leq12)$
(2)能安全通过.理由略