第138页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
变式 4 如图是一个几何体的三视图,根据图中所标数据计算这个几何体的体积为(
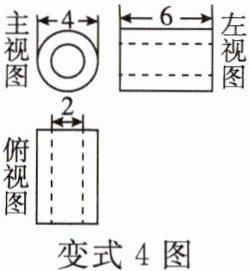
A.12π
B.18π
C.24π
D.30π
B
)
A.12π
B.18π
C.24π
D.30π
答案:
变式4 B
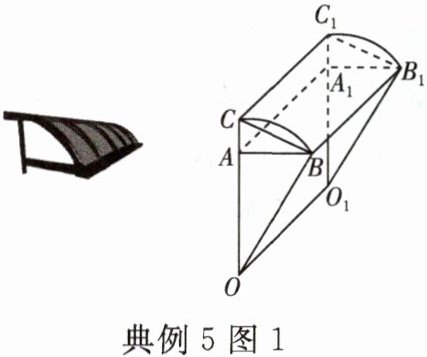
典例 5 [项目式学习]某项目学习小组研究一款挡雨棚,首先将挡雨棚抽象为柱体,如图 1 所示,底面 ABC 与 A₁B₁C₁ 全等且平行,△ABC 与△A₁B₁C₁ 各边表示挡雨棚支架,支架 AA₁,BB₁,CC₁ 垂直于平面 ABC。雨滴下落方向与外墙(所在平面)所成角为 30°(即∠AOB = 30°),挡雨棚有效遮挡的区域为矩形 AA₁O₁O(O,O₁ 分别在 CA,C₁A₁ 的延长线上)。
(1)若 OA = 1.5 m,AC = 0.3 m,AA₁ = 2 m,小组成员对曲线段 BC 有两种假设:
①挡雨板(曲面 BB₁C₁C)的面积可以近似为线段 BC 与线段 BB₁ 长的乘积,且∠ACB = 60°。
②曲线 BC 近似为以点 O 为圆心,OC 为半径的圆弧。
请分别计算这两种假设下挡雨板的面积(精确到 0.1 m²)。
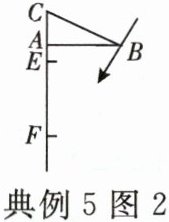
(2)如图 2,设 AB 垂直墙面(AB⊥AC),支架线段 AA₁ 下 0.1 米处有一矩形的窗,上、下窗框平行于 AA₁,上、下窗框所在直线分别与 CO 相交于点 E,F。若 AB = 0.6 m,窗的上、下框距离 EF = 1 m,请问下雨时,雨滴会打进窗内吗?若雨滴会打进窗内,请说明雨棚 AB 外沿需要加长多少米,才能使雨滴不会打进窗内;若雨滴不会打进窗内,请写出雨滴落点距点 F 的最小距离(参考数据:√3 ≈ 1.732,精确到 0.01 m)。
思维升华 当考查到平行投影时,一般将投影转化到直角三角形内,通过解直角三角形即可得出答案,解决此类问题,应多联系实际。
(1)若 OA = 1.5 m,AC = 0.3 m,AA₁ = 2 m,小组成员对曲线段 BC 有两种假设:
①挡雨板(曲面 BB₁C₁C)的面积可以近似为线段 BC 与线段 BB₁ 长的乘积,且∠ACB = 60°。
②曲线 BC 近似为以点 O 为圆心,OC 为半径的圆弧。
请分别计算这两种假设下挡雨板的面积(精确到 0.1 m²)。

(2)如图 2,设 AB 垂直墙面(AB⊥AC),支架线段 AA₁ 下 0.1 米处有一矩形的窗,上、下窗框平行于 AA₁,上、下窗框所在直线分别与 CO 相交于点 E,F。若 AB = 0.6 m,窗的上、下框距离 EF = 1 m,请问下雨时,雨滴会打进窗内吗?若雨滴会打进窗内,请说明雨棚 AB 外沿需要加长多少米,才能使雨滴不会打进窗内;若雨滴不会打进窗内,请写出雨滴落点距点 F 的最小距离(参考数据:√3 ≈ 1.732,精确到 0.01 m)。

思维升华 当考查到平行投影时,一般将投影转化到直角三角形内,通过解直角三角形即可得出答案,解决此类问题,应多联系实际。
答案:
典例5
(1)①$1.8m^{2}$ ②$1.9m^{2}$
(2)雨滴会打进窗内 雨棚AB外沿需要加长0.04m,才能使雨滴不会打进窗内
(1)①$1.8m^{2}$ ②$1.9m^{2}$
(2)雨滴会打进窗内 雨棚AB外沿需要加长0.04m,才能使雨滴不会打进窗内
例题由 5 个形状、大小完全相同的小正方体组合而成的几何体,其主视图和左视图如图所示,则搭建该几何体的方式有(
A. 1 种
B. 2 种
C. 3 种
D. 4 种
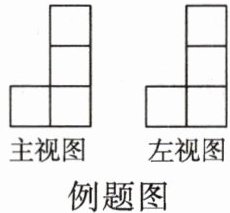
易错剖析 本题容易出错的地方在于对三视图的意义理解不透彻:(1)主视图与俯视图的列数相同,其每列方块数是俯视图中该列中各行叠放方块数量的最大值。
(2)左视图的列数与俯视图的行数相同,其每列的方块数是俯视图中该行中各列叠放方块数量的最大值。
此类问题可用口诀“俯视图打地基,主视图盖高楼,左视图拆违章”来理解。
C
)A. 1 种
B. 2 种
C. 3 种
D. 4 种

易错剖析 本题容易出错的地方在于对三视图的意义理解不透彻:(1)主视图与俯视图的列数相同,其每列方块数是俯视图中该列中各行叠放方块数量的最大值。
(2)左视图的列数与俯视图的行数相同,其每列的方块数是俯视图中该行中各列叠放方块数量的最大值。
此类问题可用口诀“俯视图打地基,主视图盖高楼,左视图拆违章”来理解。
答案:
例题 C
查看更多完整答案,请扫码查看


