第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
(2)如图 2,桌上有一个圆柱形玻璃杯(无盖)高 6 厘米,底面周长 16 厘米,在杯口内壁离杯口 1.5 厘米的$A$处有一滴蜜糖,在玻璃杯的外壁,$A$的相对方向有一小虫$P$,小虫离杯底的垂直距离为 1.5 厘米,小虫爬到蜜糖$A$处的最短距离是(

A.$\sqrt{73}$厘米
B.10 厘米
C.$8\sqrt{2}$厘米
D.8 厘米
B
)
A.$\sqrt{73}$厘米
B.10 厘米
C.$8\sqrt{2}$厘米
D.8 厘米
答案:
(2)B
(2)B
变式 4 [2025·新昌模拟]如图,长方体的长为$20\ cm$,宽为$15\ cm$,高为$10\ cm$,点$B$离点$C$为$6\ cm$,一只蚂蚁如果要沿着长方体的表面从点$A$爬到点$B$去吃一滴蜜糖,需要爬行的最短距离是(
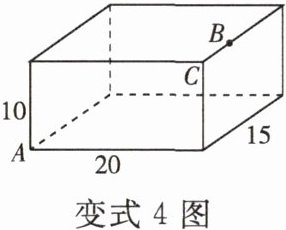
A.$5\sqrt{29}\ cm$
B.$25\ cm$
C.$2\sqrt{194}\ cm$
D.$4\sqrt{41}\ cm$
D
)
A.$5\sqrt{29}\ cm$
B.$25\ cm$
C.$2\sqrt{194}\ cm$
D.$4\sqrt{41}\ cm$
答案:
变式4 D
典例 5 如图,$\triangle ABC$是等腰直角三角形,$\angle ACB = 90^{\circ}$。$P$是$\triangle ABC$内一点,若$PA = 2.5$,$PC = \sqrt{2}$,$PB = 1.5$,则$\triangle ABC$的面积为
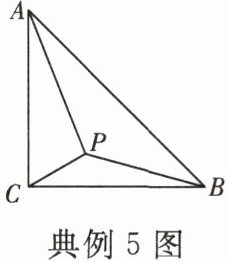
$\frac{29}{8}$
。
答案:
典例5 $\frac{29}{8}$
变式 5 [数学文化][2025·扬州]清代扬州数学家罗士琳痴迷于勾股定理的研究,提出了推算勾股数的“罗士琳法则”。法则的提出,不仅简化了勾股数的生成过程,也体现了中国传统数学在数论领域的贡献。由此法则写出了下列几组勾股数:①3,4,5;②5,12,13;③7,24,25;④9,40,41……根据上述规律,写出第 5 组勾股数:
11,60,61
。
答案:
变式5 11,60,61
典例 6 如图 1 是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成。若图 1 中大正方形的面积为 24,小正方形的面积为 4,现将这四个直角三角形拼成图 2,则图 2 中大正方形的面积为(
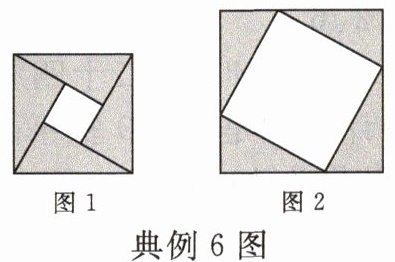
A.24
B.36
C.40
D.44
D
)
A.24
B.36
C.40
D.44
答案:
典例6 D
变式 6 - 1 [2025·拱墅区校级模拟]我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图,由弦图变化得到,它是由八个全等的直角三角形拼接而成。记图中正方形$ABCD$,正方形$EFGH$,正方形$MNKT$的面积分别为$S_1$,$S_2$,$S_3$,若$S_1 + S_2 + S_3 = 21$,则$S_2$的值是(

A.9.5
B.9
C.7.5
D.7
D
)
A.9.5
B.9
C.7.5
D.7
答案:
变式6-1 D
变式 6 - 2 [2025·上虞区模拟]如图,四个全等的直角三角形拼成“赵爽弦图”,其中四边形$ABCD$与四边形$EFGH$都是正方形。若$\tan\angle GBC = \frac{1}{2}$,则$\frac{S_{正方形EFGH}}{S_{正方形ABCD}} =$(

A.$\frac{1}{4}$
B.$\frac{1}{9}$
C.$\frac{\sqrt{5}}{5}$
D.$\frac{1}{5}$
D
)
A.$\frac{1}{4}$
B.$\frac{1}{9}$
C.$\frac{\sqrt{5}}{5}$
D.$\frac{1}{5}$
答案:
变式6-2 D
查看更多完整答案,请扫码查看


