《2026年全效学习中考学练测数学浙江专版》

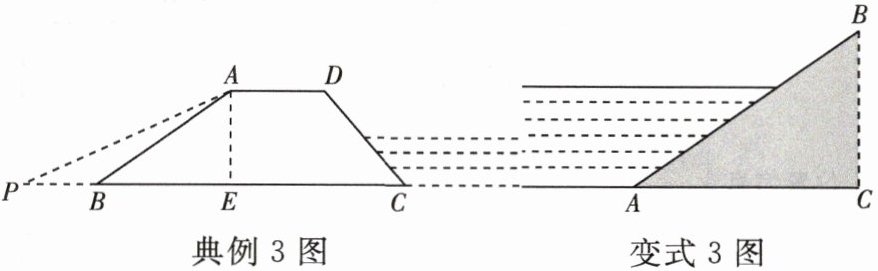
典例 3 [2025·衢州模拟]如图，一座水库大坝的横断面为梯形 $ABCD$，斜坡 $AB = 8\sqrt{3}$ m，现将坡度为 $1:\sqrt{2}$ 的斜坡 $AB$ 改为坡度为 $1:2$ 的斜坡 $AP$，则新坡面 $AP = $8\sqrt{5}$$ m。
]

答案： 典例$3 8\sqrt{5}$

变式 3 [2025·绥化]如图，某水库堤坝横断面迎水坡 $AB$ 的斜面坡度 $i = 1:\sqrt{2}$，堤坝高 $BC = 15$ m，则迎水坡面 $AB$ 的长度是 15\sqrt{3} m。
]

答案： 变式$3 15\sqrt{3}$

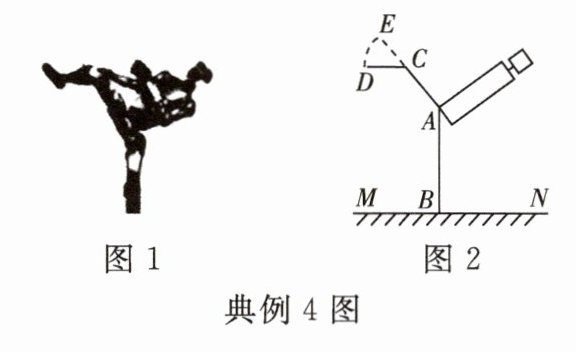
典例 4 [新情境][2025·嵊州模拟]如图 $1$ 是某科技公司机器人“G1”在展示中国功夫时的精彩瞬间，图 $2$ 是该瞬间的几何示意图，机器人的一条腿 $AB$ 直立于地面 $MN$，另一条腿的大腿部分 $AC$ 与 $AB$ 所成的角度为 $140^{\circ}$，小腿部分 $CD$ 刚好平行于地面 $MN$（即 $AB \perp MN$ 于点 $B$，$\angle CAB = 140^{\circ}$，$CD // MN$）。已知 $AB = 60$ cm，$AC = 35$ cm，$CD = 25$ cm。$CE$ 是机器人“G1”小腿 $CD$ 上踢后与大腿 $AC$ 在同一直线的瞬间（这里的小腿 $CD$，$CE$ 都包括脚面部分）。求：
（1）$\angle DCE$ 的度数。
（2）点 $E$ 距离地面的高度（结果精确到 $1$ cm。参考数据：$\sin 50^{\circ} \approx 0.766$，$\cos 50^{\circ} \approx 0.643$，$\tan 50^{\circ} \approx 1.192$）。
]

答案： 典例4
(1)50°
(2)106cm

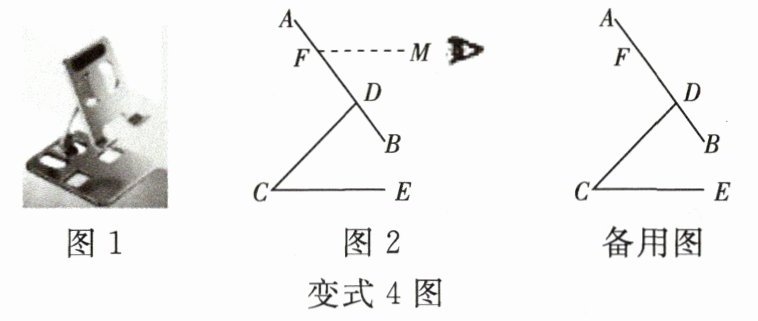
变式 4 [2025·舟山模拟]如图 $1$ 所示是一种简易手机支架，由底座、支撑板和托架组成，将手机放置在托架上，图 $2$ 是其简易结构图。现测得托架 $AB$ 长 $8$ cm，$DB$ 长 $2$ cm，支撑板 $CD$ 长 $6$ cm，$AB$ 可绕点 $D$ 转动，$CD$ 可绕点 $C$ 转动。
（1）若水平视线 $MF$ 与 $AB$ 的夹角 $\angle MFD = 50^{\circ}$，$\angle C = 35^{\circ}$，求 $\angle CDB$ 的度数。
（2）当 $\angle C = 30^{\circ}$，$\angle CDB = 80^{\circ}$ 时，求点 $A$ 到底座 $CE$ 的距离（结果精确到 $0.1$ cm，参考数据：$\sin 20^{\circ} \approx 0.34$，$\cos 20^{\circ} \approx 0.94$，$\tan 20^{\circ} \approx 0.36$）。
]

答案： 变式4
(1)95°
(2)8.6cm