第109页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
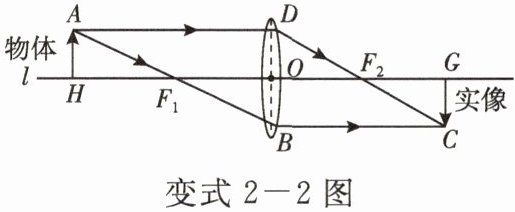
变式 2-2
[2025·金华模拟]凸透镜成像的原理如图所示,AD // 直线 l // BC,DB,AH,CG 均垂直于直线 l. 若焦点 F₁ 到物体 AH 的距离与到凸透镜的中心 O 的距离之比为 6 : 5,AH = 4 cm,则其像 CG 的长为 (
A.$\frac{5}{3}$ cm
B.3 cm
C.$\frac{10}{3}$ cm
D.$\frac{24}{5}$ cm
[2025·金华模拟]凸透镜成像的原理如图所示,AD // 直线 l // BC,DB,AH,CG 均垂直于直线 l. 若焦点 F₁ 到物体 AH 的距离与到凸透镜的中心 O 的距离之比为 6 : 5,AH = 4 cm,则其像 CG 的长为 (
C
)
A.$\frac{5}{3}$ cm
B.3 cm
C.$\frac{10}{3}$ cm
D.$\frac{24}{5}$ cm
答案:
变式2-2 C
典例 3
[2025·连云港]一块直角三角形木板,它的一条直角边 BC 长 2 m,面积为 1.5 m².
(1) 甲、乙两人分别按图 1、图 2 用它设计一个正方形桌面,请说明哪个正方形面积较大.
(2) 丙、丁两人分别按图 3、图 4 用它设计一个长方形桌面. 请分别求出图 3、图 4 中长方形的面积 y(m²)与 DE 的长 x(m)之间的函数表达式,并分别求出面积的最大值.
]
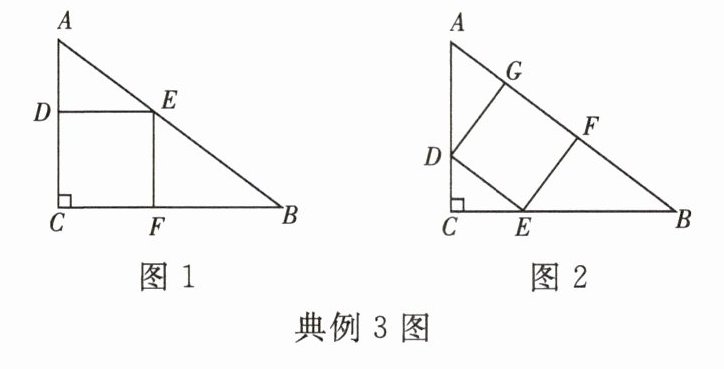
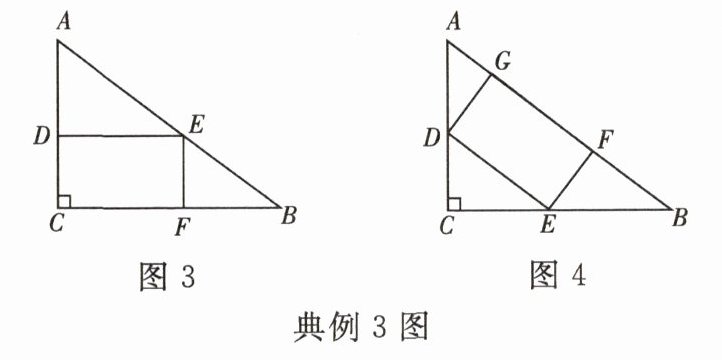
[2025·连云港]一块直角三角形木板,它的一条直角边 BC 长 2 m,面积为 1.5 m².
(1) 甲、乙两人分别按图 1、图 2 用它设计一个正方形桌面,请说明哪个正方形面积较大.
(2) 丙、丁两人分别按图 3、图 4 用它设计一个长方形桌面. 请分别求出图 3、图 4 中长方形的面积 y(m²)与 DE 的长 x(m)之间的函数表达式,并分别求出面积的最大值.
]


答案:
典例3
(1)图1的正方形面积较大
(2)略
(1)图1的正方形面积较大
(2)略
典例 4
[2025·杭州校级模拟]【课本再现】
思考:我们知道,有一组邻边相等的平行四边形叫做菱形,菱形的对角线互相垂直.
反过来,对角线互相垂直的平行四边形是菱形吗?
通过观察,可以发现并证明菱形的一个判定定理:对角线互相垂直的平行四边形是菱形.
【定理证明】(1) 为了证明该判定定理,小南同学画出了图形(如图 1),并写出了“已知”和“求证”,请根据定义完成证明过程.
已知:在□ABCD 中,对角线 BD⊥AC,垂足为 O.
求证:□ABCD 是菱形.
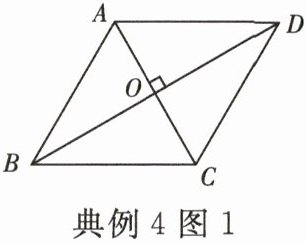
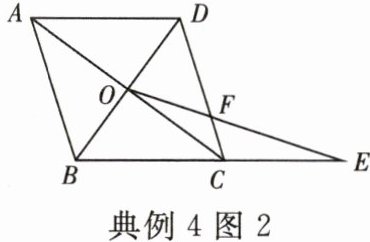
【知识应用】(2) 如图 2,在□ABCD 中,对角线 AC 和 BD 相交于点 O,AD = 10,AC = 16,BD = 12.
① 求证:□ABCD 是菱形.
② 延长 BC 至点 E,连结 OE,交 CD 于点 F,若 ∠E = $\frac{1}{2}$∠ACD,求 $\frac{OF}{EF}$ 的值.
]
[2025·杭州校级模拟]【课本再现】
思考:我们知道,有一组邻边相等的平行四边形叫做菱形,菱形的对角线互相垂直.
反过来,对角线互相垂直的平行四边形是菱形吗?
通过观察,可以发现并证明菱形的一个判定定理:对角线互相垂直的平行四边形是菱形.
【定理证明】(1) 为了证明该判定定理,小南同学画出了图形(如图 1),并写出了“已知”和“求证”,请根据定义完成证明过程.
已知:在□ABCD 中,对角线 BD⊥AC,垂足为 O.
求证:□ABCD 是菱形.

【知识应用】(2) 如图 2,在□ABCD 中,对角线 AC 和 BD 相交于点 O,AD = 10,AC = 16,BD = 12.
① 求证:□ABCD 是菱形.
② 延长 BC 至点 E,连结 OE,交 CD 于点 F,若 ∠E = $\frac{1}{2}$∠ACD,求 $\frac{OF}{EF}$ 的值.
]

答案:
典例4
(1)略
(2)①略 ②$\frac{5}{8}$
(1)略
(2)①略 ②$\frac{5}{8}$
查看更多完整答案,请扫码查看


