第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
8. [2023·北京]在平面直角坐标系中,函数y=kx+b(k≠0)的图象经过点A(0,1)和B(1,2),与过点(0,4)且平行于x轴的直线交于点C。
(1)求该函数的表达式及点C的坐标;
(2)当x<3时,对于x的每一个值,函数y=$\frac{2}{3}$x+n的值大于函数y=kx+b(k≠0)的值且小于4,直接写出n的值。
(1)求该函数的表达式及点C的坐标;
(2)当x<3时,对于x的每一个值,函数y=$\frac{2}{3}$x+n的值大于函数y=kx+b(k≠0)的值且小于4,直接写出n的值。
答案:
8.
(1)该函数的表达式为y=x+1。C(3,4)。
(2)n=2
(1)该函数的表达式为y=x+1。C(3,4)。
(2)n=2
9. [2023·绍兴]一条笔直的路上依次有M,P,N三地,其中M,N两地相距1000m。甲、乙两机器人分别从M,N两地同时出发,匀速去目的地N,M。图中OA,BC分别表示甲、乙机器人离M地的距离y(单位:m)与行走时间x(单位:min)的函数关系图象。
(1)求OA所在直线的表达式。
(2)出发后甲机器人行走多少时间,与乙机器人相遇?
(3)甲机器人到P地后,再经过1min乙机器人也到P地,求P,M两地间的距离。
 ]
]
(1)求OA所在直线的表达式。
(2)出发后甲机器人行走多少时间,与乙机器人相遇?
(3)甲机器人到P地后,再经过1min乙机器人也到P地,求P,M两地间的距离。
 ]
]
答案:
9.
(1)OA所在直线的表达式为y=200x。
(2)出发后甲机器人行走$\frac{10}{3}min,$与乙机器人相遇。
(3)P,M两地间的距离为600m。
(1)OA所在直线的表达式为y=200x。
(2)出发后甲机器人行走$\frac{10}{3}min,$与乙机器人相遇。
(3)P,M两地间的距离为600m。
10. [2023·广西]【综合与实践】某兴趣小组将利用物理学中杠杆原理制作简易杆秤,小组先设计方案,然后动手制作,再结合实际进行调试,请完成下列方案设计中的任务。
【知识背景】如图,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得$(m_0 + m)·l = M·(a + y)$,其中秤盘质量m₀g,重物质量mg,秤砣质量Mg,秤纽与秤盘的水平距离为lcm,秤纽与零刻线的水平距离为acm,秤砣与零刻线的水平距离为ycm。
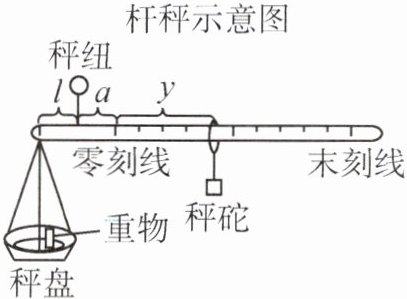
【方案设计】目标:设计简易杆秤。设定m₀=10,M=50,最大可称重物质量为1000g,零刻线与末刻线的距离定为50cm。
任务一:确定l和a的值。
(1)当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于l,a的方程;
(2)当秤盘放入质量为1000g的重物,秤砣从零刻线移至末刻线时,杆秤平衡,请列出关于l,a的方程;
(3)根据(1)和(2)所列方程,求出l和a的值;
任务二:确定刻线的位置。
(4)根据任务一,求y关于m的函数表达式;
(5)从零刻线开始,每隔100g在秤杆上找到对应刻线,请写出相邻刻线间的距离。
【知识背景】如图,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得$(m_0 + m)·l = M·(a + y)$,其中秤盘质量m₀g,重物质量mg,秤砣质量Mg,秤纽与秤盘的水平距离为lcm,秤纽与零刻线的水平距离为acm,秤砣与零刻线的水平距离为ycm。

【方案设计】目标:设计简易杆秤。设定m₀=10,M=50,最大可称重物质量为1000g,零刻线与末刻线的距离定为50cm。
任务一:确定l和a的值。
(1)当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于l,a的方程;
(2)当秤盘放入质量为1000g的重物,秤砣从零刻线移至末刻线时,杆秤平衡,请列出关于l,a的方程;
(3)根据(1)和(2)所列方程,求出l和a的值;
任务二:确定刻线的位置。
(4)根据任务一,求y关于m的函数表达式;
(5)从零刻线开始,每隔100g在秤杆上找到对应刻线,请写出相邻刻线间的距离。
答案:
10.
(1)l=5a
(2)101l-5a=250
(3)a=0.5,l=2.5
(4)y=0.05m
(5)相邻刻线间的距离为5cm。
(1)l=5a
(2)101l-5a=250
(3)a=0.5,l=2.5
(4)y=0.05m
(5)相邻刻线间的距离为5cm。
查看更多完整答案,请扫码查看


