第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
3. 已知图中数字表示对应正方形的面积,则$S_{正方形A}=$
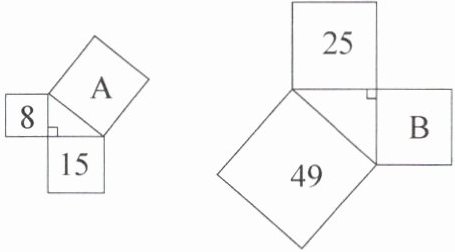
23
,$S_{正方形B}=$24
。
答案:
3.23 24
1. 如图,湖的两端有$A$,$B$两点,从与$BA$方向垂直的$BC$方向上的点$C$测得$CA = 130m$,$CB = 120m$,则$AB$的长为(
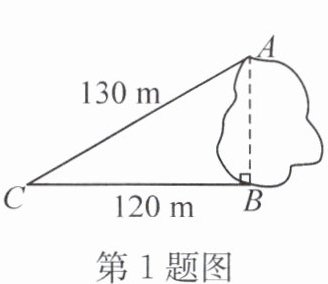
A.$50m$
B.$120m$
C.$100m$
D.$130m$
A
)
A.$50m$
B.$120m$
C.$100m$
D.$130m$
答案:
1.A
2. [2024秋·沈阳月考]如图,长方形$BCFG$是一块草地,折线$ABCDE$是一条人行道,$BC = 15m$,$CD = 8m$,为了避免行人穿过草地(走虚线$BD$),践踏绿草,管理部门分别在$B$,$D$处各挂了一块牌子,牌子上写着“少走
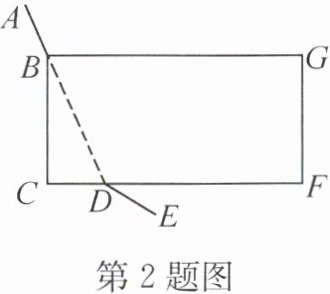
A.$5$
B.$6$
C.$4$
D.$7$
6
$m$,踏之何忍”,则横线上应填(B
)
A.$5$
B.$6$
C.$4$
D.$7$
答案:
2.B
3. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AB = 10cm$,$BC = 6cm$,$CD\perp AB$,垂足为$D$。求:
(1)$AC$的长;
(2)$\triangle ABC$的面积;
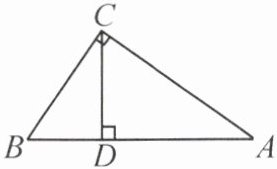
(3)$CD$的长。
(1)$AC$的长;
(2)$\triangle ABC$的面积;

(3)$CD$的长。
答案:
3.
(1)$AC = 8\ cm$
(2)$S_{\triangle ABC}=24\ cm^{2}$
(3)$CD = \frac{24}{5}\ cm$
(1)$AC = 8\ cm$
(2)$S_{\triangle ABC}=24\ cm^{2}$
(3)$CD = \frac{24}{5}\ cm$
4. 如图,分别以$Rt\triangle ABC$的三边为边长向外侧作正方形,面积分别记为$S_{1}$,$S_{2}$,$S_{3}$。若$S_{3}+S_{2}-S_{1}=20$,则图中阴影部分的面积为(
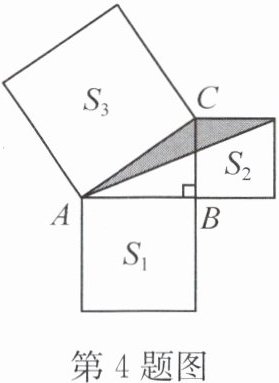
A.$5$
B.$10$
C.$15$
D.$20$
A
)
A.$5$
B.$10$
C.$15$
D.$20$
答案:
4.A
5. [2024秋·苏家屯区校级期末]如图,正方形$ABCD$的边长为$2$,其面积记为$S_{1}$,以$AB$为斜边向外作等腰直角三角形,再以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为$S_{2}\cdots\cdots$按照此规律继续下去,则$S_{8}$的值为
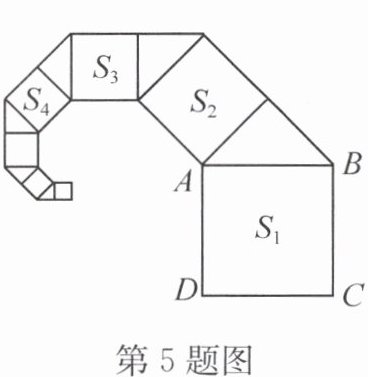
$\frac{1}{32}$
。
答案:
5.$\frac{1}{32}$
6. (模型观念)如图1,有一个面积为$1$的正方形,经过一次“生长”后,在它的左右肩上长出两个小正方形,且三个正方形围成的三角形是直角三角形,如图2所示。再经过一次“生长”后,变成图3……如果继续“生长”下去,它将变得更加“枝繁叶茂”。随着不断地“生长”,形成的图形中所有正方形的面积和也随之变化。若生长$n$次后(如图4),变成的图形中所有正方形的面积用$S_{n}$表示,则$S_{n}=$
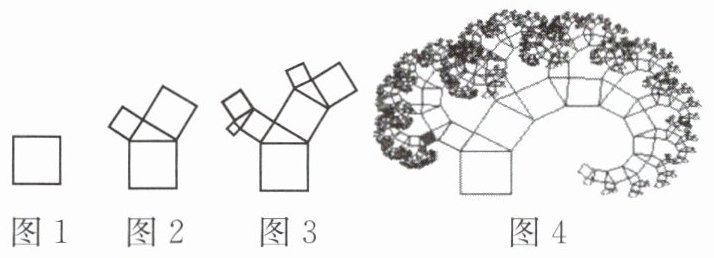
$n + 1$
。
答案:
6.$n + 1$
查看更多完整答案,请扫码查看


