《2025年全效学习学业评价方案八年级数学上册北师大版》

1. 众数
定 义：一组数据中出现次数最多的那个数据叫作这组数据的众数。
注 意：一组数据的众数有时可能不止一个。
2. 算术平均数
定 义：一般地，对于 $ n $ 个数 $ x_{1},x_{2},\cdots,x_{n} $，我们把$\frac{1}{n}(x_1 + x_2 + \cdots + x_n)$叫作这 $ n $ 个数的算术平均数，简称平均数，记为$\bar{x}$。

答案： 1. 出现次数最多 2.$\frac{1}{n}(x_1 + x_2 + \cdots + x_n)$ $\bar{x}$

例 1 [2024 秋·于洪区期末]某鞋店在一周内销售了 30 双鞋，各种尺码的销售量如下表：

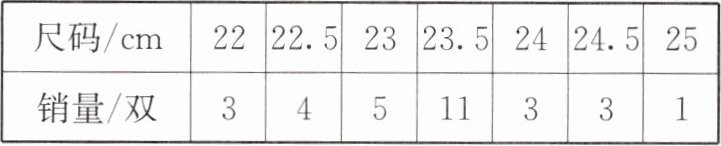
该鞋店下一周进鞋最多的尺码应是23.5cm。

答案： 【例1】23.5

例 2 [2024 春·德化县期末]已知一组 10 个数据：0，1，3，3，3，5，6，7，9，10，在计算这组数据的平均数时，甲、乙、丙三位同学分别列出了如下不同的算式。
甲：$(1 + 3 + 3 + 3 + 5 + 6 + 7 + 9 + 10)÷ 9$；
乙：$(0 + 1 + 3 + 5 + 6 + 7 + 9 + 10)÷ 8$；
丙：$(0 + 1 + 3× 3 + 5 + 6 + 7 + 9 + 10)÷ 10$。
其中算式正确的是丙。(填“甲”“乙”或“丙”)

答案： 【例2】丙

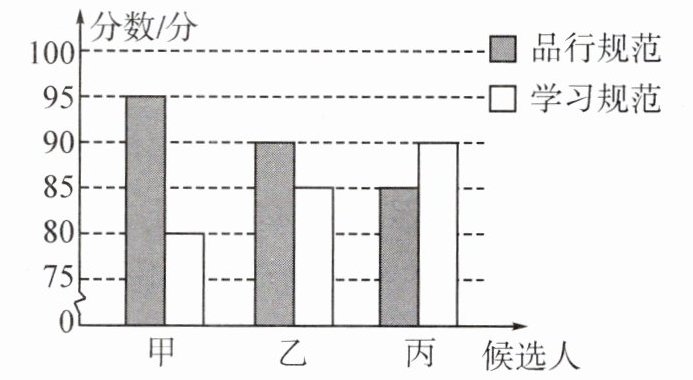
例 3 某校德育处组织三好学生评比活动，每班只有一个名额。现某班有甲、乙、丙三名学生参与竞选，根据“品行规范”“学习规范”进行量化考核，成绩（单位：分）统计如图所示。要求“品行规范”“学习规范”考核成绩均不低于三名学生的平均分的学生，才能被推选为三好学生，请通过计算判断应推选谁为三好学生？

答案： 【例3】应推选乙为三好学生。