第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
例3 [2024秋·沈北新区校级期中]把下列各数分类,并填在表示相应集合的大括号里。
$-3$,$+\frac{1}{5}$,0.1,9,0,1.23,$-4\frac{1}{3}$,10%,$\pi$。
(1)正数集合:{ ,…};
(2)正整数集合:{ ,…};
(3)负分数集合:{ ,…}。
$-3$,$+\frac{1}{5}$,0.1,9,0,1.23,$-4\frac{1}{3}$,10%,$\pi$。
(1)正数集合:{ ,…};
(2)正整数集合:{ ,…};
(3)负分数集合:{ ,…}。
答案:
(1)$+\frac{1}{5}$,0.1,9,1.23,10%,π
(2)9
(3)$-4\frac{1}{3}$
(1)$+\frac{1}{5}$,0.1,9,1.23,10%,π
(2)9
(3)$-4\frac{1}{3}$
例4 如图,圆的直径为1个单位长度,该圆上的点A与数轴上的原点重合,将此圆沿数轴负方向滚动1周,点A到达点B的位置,点B表示的数为(
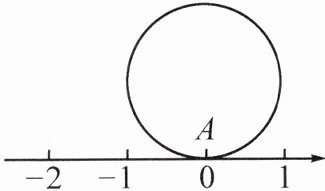
A.$\pi$
B.$-\pi$
C.1
D.$\pi$
B
)
A.$\pi$
B.$-\pi$
C.1
D.$\pi$
答案:
B
1. 下列各数中,属于无理数的是(
A.2
B.$\pi$
C.$\frac{3}{2}$
D.-2
B
)A.2
B.$\pi$
C.$\frac{3}{2}$
D.-2
答案:
1.B
2. 下列说法正确的是(
A.有理数只是有限小数
B.无理数是无限不循环小数
C.$\frac{1}{3}$是无理数
D.$\frac{\pi}{3}$是有理数
B
)A.有理数只是有限小数
B.无理数是无限不循环小数
C.$\frac{1}{3}$是无理数
D.$\frac{\pi}{3}$是有理数
答案:
2.B
3. $-\sqrt{11}$的绝对值的3倍与$4\sqrt{11}$的差的相反数等于(
A.$\sqrt{11}$
B.$-\sqrt{11}$
C.1
D.-1
A
)A.$\sqrt{11}$
B.$-\sqrt{11}$
C.1
D.-1
答案:
3.A
4. 写出一个比4小的正无理数:
π
。
答案:
4.π(答案不唯一)
5. 在$\frac{3}{7}$,$-\pi$,0.5252252225…(相邻两个5之间2的个数逐次加1),0,0.3,$\frac{\pi}{2}$,0.33中,
属于有理数的有
属于无理数的有
属于有理数的有
$\frac{3}{7}$,0,0.3,0.33
;属于无理数的有
$-\pi$,0.5252252225…(相邻两个5之间2的个数逐次加1),$\frac{\pi}{2}$
。
答案:
5.$\frac{3}{7}$,0,0.3,0.33;$-\pi$,0.5252252225…(相邻两个5之间2的个数逐次加1),$\frac{\pi}{2}$
1. 面积为7的正方形的边长是(
A.整数
B.分数
C.有理数
D.无理数
D
)A.整数
B.分数
C.有理数
D.无理数
答案:
1.D
2. 在如图所示的正方形网格中,每个小正方形的边长都为1,$\triangle ABC$的顶点都在网格上,则长度为有理数的边有(
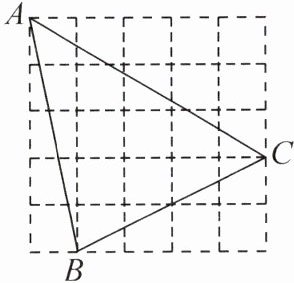
A.0条
B.1条
C.2条
D.3条
A
)
A.0条
B.1条
C.2条
D.3条
答案:
2.A
3. 已知$43^2 = 1849$,$44^2 = 1936$,$45^2 = 2025$,$46^2 = 2116$。若n为整数且$n^2 < 2026 < (n + 1)^2$,则n的值为(
A.43
B.44
C.45
D.46
C
)A.43
B.44
C.45
D.46
答案:
3.C
4. 等边三角形的边长为6,高为h,则$h^2 =$
27
,若精确到个位,则h约为5
。
答案:
4.27 5
5. 如图,数轴上点O,A所表示的数分别是0,3,过点A作AB垂直于数轴,$AB = 1$,以O为圆心,OB的长为半径画弧交数轴于点C(位于点A左侧),则点C表示的数是______。
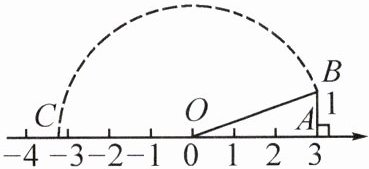

答案:
5.$-\sqrt{10}$
6. [2024·皇姑区校级月考]把下列各数填入相应的集合内。
3,-7,$-\frac{2}{3}$,$5.\dot{6}$,0,$-8\frac{1}{4}$,15,$\frac{1}{9}$,$\frac{\pi}{3}$,0.1010010001…(相邻两个1之间0的个数逐次加1),3.1415926。
正数集合:{ ,…};
负数集合:{ ,…};
分数集合:{ ,…}。
3,-7,$-\frac{2}{3}$,$5.\dot{6}$,0,$-8\frac{1}{4}$,15,$\frac{1}{9}$,$\frac{\pi}{3}$,0.1010010001…(相邻两个1之间0的个数逐次加1),3.1415926。
正数集合:{ ,…};
负数集合:{ ,…};
分数集合:{ ,…}。
答案:
6.正数集合:{3,5.6,15,$\frac{1}{9}$,$\frac{\pi}{3}$,0.1010010001…(相邻两个1之间0的个数逐次加1),3.1415926,…};
负数集合:{-7,$-\frac{2}{3}$,$-8\frac{1}{4}$,…};
分数集合:{$-\frac{2}{3}$,5.$\overset{.}{6}$,$-8\frac{1}{4}$,$\frac{1}{9}$,3.1415926,…}。
负数集合:{-7,$-\frac{2}{3}$,$-8\frac{1}{4}$,…};
分数集合:{$-\frac{2}{3}$,5.$\overset{.}{6}$,$-8\frac{1}{4}$,$\frac{1}{9}$,3.1415926,…}。
查看更多完整答案,请扫码查看


