第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
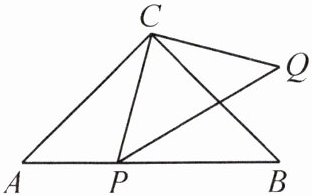
5. 如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ AC = BC $,点 $ P $ 在斜边 $ AB $ 上,以 $ PC $ 为直角边作等腰直角三角形 $ PCQ $,$ \angle PCQ = 90^{\circ} $,试探索 $ PA^{2} $,$ PB^{2} $,$ PC^{2} $ 三者之间的数量关系,并说明理由。

答案:
$PA^{2} + PB^{2} = 2PC^{2}$
证明:连接 $QB$。
因为 $\angle ACB = 90^{\circ}$,$AC = BC$,所以 $\angle A = \angle ABC = 45^{\circ}$。
因为 $\triangle PCQ$ 是等腰直角三角形,$\angle PCQ = 90^{\circ}$,所以 $PC = QC$,$\angle PCQ = 90^{\circ}$。
所以 $\angle ACB = \angle PCQ$,则 $\angle ACB - \angle PCB = \angle PCQ - \angle PCB$,即 $\angle ACP = \angle BCQ$。
在 $\triangle ACP$ 和 $\triangle BCQ$ 中,$\left\{\begin{array}{l} AC = BC \\ \angle ACP = \angle BCQ \\ PC = QC \end{array}\right.$,所以 $\triangle ACP \cong \triangle BCQ(SAS)$。
所以 $PA = QB$,$\angle A = \angle CBQ = 45^{\circ}$。
所以 $\angle ABQ = \angle ABC + \angle CBQ = 45^{\circ} + 45^{\circ} = 90^{\circ}$。
在 $Rt\triangle PBQ$ 中,$PB^{2} + QB^{2} = PQ^{2}$。
因为 $PA = QB$,所以 $PB^{2} + PA^{2} = PQ^{2}$。
在等腰直角三角形 $PCQ$ 中,$PQ^{2} = PC^{2} + QC^{2} = 2PC^{2}$。
所以 $PA^{2} + PB^{2} = 2PC^{2}$。
6. 如图,在 $ \triangle ABC $ 中,$ D $ 是 $ AB $ 边的中点,$ DE \perp AB $ 于点 $ D $,交 $ AC $ 于点 $ E $,且 $ AE^{2} - CE^{2} = BC^{2} $。
(1)试说明 $ \angle C = 90^{\circ} $;
(2)若 $ DE = 6 $,$ BD = 8 $,求 $ CE $ 的长。
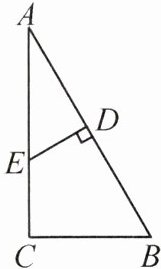
(1)试说明 $ \angle C = 90^{\circ} $;
(2)若 $ DE = 6 $,$ BD = 8 $,求 $ CE $ 的长。

答案:
1. (1)
解:连接$BE$。
因为$D$是$AB$边的中点,$DE\perp AB$,根据线段垂直平分线的性质,可得$AE = BE$。
已知$AE^{2}-CE^{2}=BC^{2}$,将$AE = BE$代入可得:$BE^{2}-CE^{2}=BC^{2}$。
根据勾股定理的逆定理,在$\triangle BCE$中,若$a^{2}+b^{2}=c^{2}$(这里$a = BC$,$b = CE$,$c = BE$),则$\angle C = 90^{\circ}$。
2. (2)
解:因为$D$是$AB$边的中点,$BD = 8$,所以$AB=2BD = 16$。
又因为$DE\perp AB$,$DE = 6$,在$Rt\triangle BDE$中,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$a = DE$,$b = BD$,$c = BE$),可得$BE=\sqrt{BD^{2}+DE^{2}}=\sqrt{8^{2}+6^{2}}=\sqrt{64 + 36}=\sqrt{100}=10$。
所以$AE = BE = 10$。
设$CE=x$,则$AC=AE + CE=10 + x$,$BC^{2}=BE^{2}-CE^{2}=100-x^{2}$。
在$Rt\triangle ABC$中,$AB = 16$,$AC=10 + x$,$BC^{2}=100 - x^{2}$,根据勾股定理$AC^{2}+BC^{2}=AB^{2}$,即$(10 + x)^{2}+100 - x^{2}=16^{2}$。
展开$(10 + x)^{2}+100 - x^{2}=16^{2}$得:$100+20x+x^{2}+100 - x^{2}=256$。
化简得:$20x+200 = 256$。
移项得:$20x=256 - 200$,即$20x=56$。
解得$x=\frac{56}{20}=\frac{14}{5}$。
所以(1)通过连接$BE$,利用线段垂直平分线性质和勾股定理逆定理可证$\angle C = 90^{\circ}$;(2)$CE$的长为$\frac{14}{5}$。
解:连接$BE$。
因为$D$是$AB$边的中点,$DE\perp AB$,根据线段垂直平分线的性质,可得$AE = BE$。
已知$AE^{2}-CE^{2}=BC^{2}$,将$AE = BE$代入可得:$BE^{2}-CE^{2}=BC^{2}$。
根据勾股定理的逆定理,在$\triangle BCE$中,若$a^{2}+b^{2}=c^{2}$(这里$a = BC$,$b = CE$,$c = BE$),则$\angle C = 90^{\circ}$。
2. (2)
解:因为$D$是$AB$边的中点,$BD = 8$,所以$AB=2BD = 16$。
又因为$DE\perp AB$,$DE = 6$,在$Rt\triangle BDE$中,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$a = DE$,$b = BD$,$c = BE$),可得$BE=\sqrt{BD^{2}+DE^{2}}=\sqrt{8^{2}+6^{2}}=\sqrt{64 + 36}=\sqrt{100}=10$。
所以$AE = BE = 10$。
设$CE=x$,则$AC=AE + CE=10 + x$,$BC^{2}=BE^{2}-CE^{2}=100-x^{2}$。
在$Rt\triangle ABC$中,$AB = 16$,$AC=10 + x$,$BC^{2}=100 - x^{2}$,根据勾股定理$AC^{2}+BC^{2}=AB^{2}$,即$(10 + x)^{2}+100 - x^{2}=16^{2}$。
展开$(10 + x)^{2}+100 - x^{2}=16^{2}$得:$100+20x+x^{2}+100 - x^{2}=256$。
化简得:$20x+200 = 256$。
移项得:$20x=256 - 200$,即$20x=56$。
解得$x=\frac{56}{20}=\frac{14}{5}$。
所以(1)通过连接$BE$,利用线段垂直平分线性质和勾股定理逆定理可证$\angle C = 90^{\circ}$;(2)$CE$的长为$\frac{14}{5}$。
7. [2024·和平区校级月考]如图,已知在长方形 $ ABCD $ 中,$ AB = 3 cm $,$ AD = 9 cm $,将此长方形折叠,使点 $ B $ 与点 $ D $ 重合,折痕为 $ EF $,则 $ \triangle ABE $ 的面积为
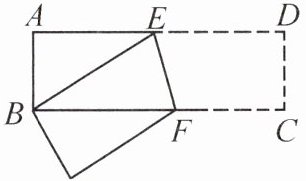
6 cm^2
。
答案:
$7.6 cm^2$
8. 如图是一个供滑板爱好者使用的 $ U $ 型池,该 $ U $ 型池可以看作是一个长方体去掉一个半圆柱而成,中间可供滑行部分的横截面是半径为 $ 3 m $ 的半圆,该部分的边缘 $ AB = CD = 15 m $,点 $ E $ 在 $ CD $ 上,$ CE = 3 m $,一滑行爱好者从 $ A $ 点到 $ E $ 点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,$ \pi $ 取整数 3)
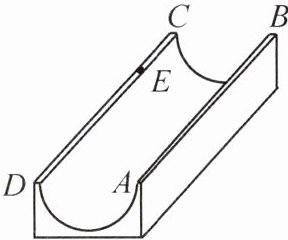

答案:
8. 他滑行的最短距离约为15 m。
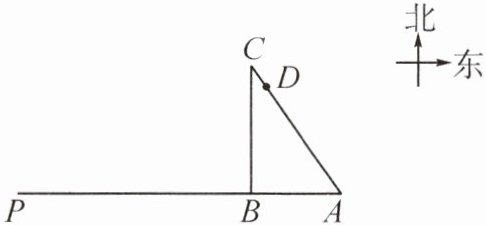
9. 张丘建是我国著名的数学家,著有《张丘建算经》。一次宴会上,张丘建出了一道题:“现有一只鹿向西跑,当猎人追至 $ A $ 处时,与鹿所在的 $ B $ 处还差 36 步(“步”是我国古代长度单位,1 里 $ = 300 $ 步);此时鹿突然向北跑,猎人就沿着 $ AD $ 追去,追了 50 步至 $ D $ 处与鹿所在的位置 $ C $ 处还差 10 步(点 $ A $,$ C $,$ D $ 在同一直线上)。如果此鹿一开始就不向北转,而是继续向西跑,猎人需要追多远才能追上此鹿?”已知单位时间内鹿跑的路程和猎人追赶的路程的比值是定值,请解答这个问题。

答案:
9. 猎人需要追900步才能追上此鹿。
查看更多完整答案,请扫码查看


