第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
6. (创新意识、模型观念)[2024秋·扶风县期中]先阅读下面的材料,再解决问题。
【实际问题】如图1,一圆柱的底面半径为5cm,BC是底面直径,高AB为5cm,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线。
【解决方案】小明设计了两条路线。
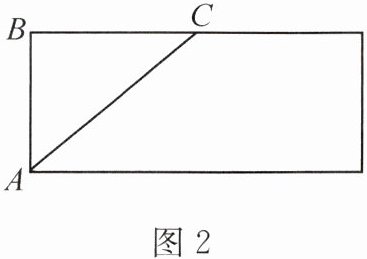
路线1:沿AB剪开摊平,如图2,侧面展开图中的线段AC即为所求路线。
∵底面半径为5cm,
∴底面周长为10π,
∴BC=5π,
设路线1的长度为l₁,则l₁²=AC²=AB²+BC²=5²+(5π)²=25+25π²。
路线2:高线AB+底面直径BC。
设路线2的长度为l₂,则l₂²=(AB+BC)²=(5+10)²=225。
为比较l₁,l₂的大小,采用“作差法”:
∵l₁²-l₂²=25(π²-8)>0,∴l₁²>l₂²,
∴l₁>l₂,
∴小明认为路线2较短。
【问题类比】(1)小亮对上述结论有些疑惑,于是他把条件改成“圆柱的底面半径为1cm,高AB为5cm”。请你用上述方法帮小亮比较出哪条路线更短。
【问题拓展】(2)请你继续研究:在一般情况下,若圆柱的底面半径为rcm,高为hcm,蚂蚁从点A出发沿圆柱表面爬行到点C,当r/h满足什么条件时,路线2较短? 请说明理由。
【问题解决】(3)如图3是紧密排列在一起的两个相同的圆柱,高为5cm。当蚂蚁从点A出发沿圆柱表面爬行到点C的两条路线长度相等时,求圆柱的底面半径r。
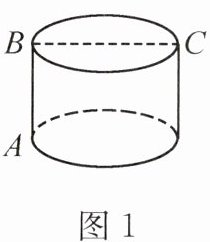

【实际问题】如图1,一圆柱的底面半径为5cm,BC是底面直径,高AB为5cm,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线。
【解决方案】小明设计了两条路线。
路线1:沿AB剪开摊平,如图2,侧面展开图中的线段AC即为所求路线。
∵底面半径为5cm,
∴底面周长为10π,
∴BC=5π,
设路线1的长度为l₁,则l₁²=AC²=AB²+BC²=5²+(5π)²=25+25π²。
路线2:高线AB+底面直径BC。
设路线2的长度为l₂,则l₂²=(AB+BC)²=(5+10)²=225。
为比较l₁,l₂的大小,采用“作差法”:
∵l₁²-l₂²=25(π²-8)>0,∴l₁²>l₂²,
∴l₁>l₂,
∴小明认为路线2较短。
【问题类比】(1)小亮对上述结论有些疑惑,于是他把条件改成“圆柱的底面半径为1cm,高AB为5cm”。请你用上述方法帮小亮比较出哪条路线更短。
【问题拓展】(2)请你继续研究:在一般情况下,若圆柱的底面半径为rcm,高为hcm,蚂蚁从点A出发沿圆柱表面爬行到点C,当r/h满足什么条件时,路线2较短? 请说明理由。
【问题解决】(3)如图3是紧密排列在一起的两个相同的圆柱,高为5cm。当蚂蚁从点A出发沿圆柱表面爬行到点C的两条路线长度相等时,求圆柱的底面半径r。



答案:
6.
(1)路线1较短。
(2)当$\frac{r}{h}>\frac{4}{\pi^{2}-4}$时,路线2较短。
(3)$r=\frac{10}{\pi^{2}-4}$
(1)路线1较短。
(2)当$\frac{r}{h}>\frac{4}{\pi^{2}-4}$时,路线2较短。
(3)$r=\frac{10}{\pi^{2}-4}$
查看更多完整答案,请扫码查看


