第124页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
1. 调查了五名同学一周的零花钱使用情况,分别为 30,35,30,40,20(单位:元)。这组数据的众数是(
A.20
B.30
C.35
D.40
B
)A.20
B.30
C.35
D.40
答案:
1.B
2. 在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数。若去掉一个最高分,平均分为 $ x $;去掉一个最低分,平均分为 $ y $;同时去掉一个最高分和一个最低分,平均分为 $ z $,则(
A.$ y>z>x $
B.$ x>z>y $
C.$ y>x>z $
D.$ z>y>x $
A
)A.$ y>z>x $
B.$ x>z>y $
C.$ y>x>z $
D.$ z>y>x $
答案:
2.A
3. [2023·丽水]青田县“稻鱼共生”种养方式因稻鱼双收、互惠共生而受到农户青睐,现有一农户在 5 块面积相等的稻田里养殖田鱼,产量分别是(单位:kg):12,13,15,17,18,则这 5 块稻田的田鱼平均产量是
15
kg。
答案:
3.15
1. 某 4S 店今年 1 月至 5 月新能源汽车的销量(单位:辆)分别如下:25,33,36,31,40。这组数据的平均数是(
A.34
B.33
C.32.5
D.31
B
)A.34
B.33
C.32.5
D.31
答案:
1.B
2. [2025·鹿城区校级期初]某班 40 名学生一周阅读书籍的册数统计图如图所示,该班阅读书籍的册数的众数是(
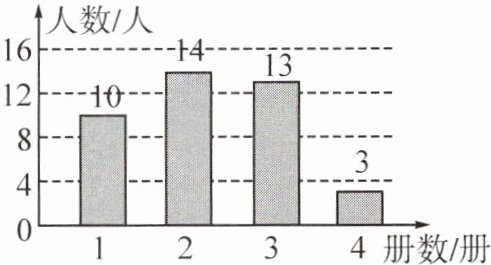
A.1 册
B.2 册
C.3 册
D.4 册
B
)
A.1 册
B.2 册
C.3 册
D.4 册
答案:
2.B
3. “活力东部新区,运动未来之城”,2024 年 11 月 22 日至 24 日,成都东部新区第二届中小学生田径运动会在成都东部新区某校隆重举行。本次运动会中,参加男子跳远的 15 名中学生运动员的身高如表所示:

这些运动员身高的众数是(
A.1.72
B.1.73
C.1.75
D.1.76

这些运动员身高的众数是(
A
)A.1.72
B.1.73
C.1.75
D.1.76
答案:
3.A
4. [2024·宿迁]一组数据 6,8,10,$ x $ 的平均数是 9,则 $ x $ 的值为
12
。
答案:
4.12
5. 已知一组数据 $ a_{1},a_{2},a_{3},a_{4},a_{5} $ 的平均数是 8,则另一组数据 $ a_{1} + 10,a_{2} - 10,a_{3} + 10,a_{4} - 10,a_{5} + 10 $ 的平均数为
10
。
答案:
5.10
6. (数据观念)[2024·福建]已知 A,B 两地都只有甲、乙两类普通高中学校。在一次普通高中学业水平考试中,A 地甲类学校有考生 3000 人,数学平均分为 90 分,乙类学校有考生 2000 人,数学平均分为 80 分。
(1)求 A 地考生的数学平均分。
(2)若 B 地甲类学校数学平均分为 94 分,乙类学校数学平均分为 82 分,据此,能否判断 B 地考生数学平均分一定比 A 地考生数学平均分高?若能,请给予说明;若不能,请举例说明。
(1)求 A 地考生的数学平均分。
(2)若 B 地甲类学校数学平均分为 94 分,乙类学校数学平均分为 82 分,据此,能否判断 B 地考生数学平均分一定比 A 地考生数学平均分高?若能,请给予说明;若不能,请举例说明。
答案:
1. (1)
解:根据加权平均数公式$\overline{x}=\frac{x_1n_1 + x_2n_2}{n_1 + n_2}$(其中$x_1$,$x_2$为不同组的平均数,$n_1$,$n_2$为不同组的数量)。
已知$n_1 = 3000$,$x_1 = 90$,$n_2 = 2000$,$x_2 = 80$。
则$A$地考生的数学平均分$\overline{x}=\frac{90×3000 + 80×2000}{3000 + 2000}$
先计算分子:$90×3000+80×2000=270000 + 160000=430000$。
再计算分母:$3000 + 2000 = 5000$。
所以$\overline{x}=\frac{430000}{5000}=86$(分)。
2. (2)
解:不能判断$B$地考生数学平均分一定比$A$地考生数学平均分高。
举例:设$B$地甲类学校有考生$1000$人,乙类学校有考生$4000$人。
根据加权平均数公式$\overline{y}=\frac{94×1000+82×4000}{1000 + 4000}$。
先计算分子:$94×1000+82×4000=94000+328000 = 422000$。
再计算分母:$1000 + 4000 = 5000$。
则$\overline{y}=\frac{422000}{5000}=84.4$分。
因为$84.4\lt86$,所以不能判断$B$地考生数学平均分一定比$A$地考生数学平均分高。
综上,(1)$A$地考生的数学平均分是$86$分;(2)不能判断,如上述举例。
解:根据加权平均数公式$\overline{x}=\frac{x_1n_1 + x_2n_2}{n_1 + n_2}$(其中$x_1$,$x_2$为不同组的平均数,$n_1$,$n_2$为不同组的数量)。
已知$n_1 = 3000$,$x_1 = 90$,$n_2 = 2000$,$x_2 = 80$。
则$A$地考生的数学平均分$\overline{x}=\frac{90×3000 + 80×2000}{3000 + 2000}$
先计算分子:$90×3000+80×2000=270000 + 160000=430000$。
再计算分母:$3000 + 2000 = 5000$。
所以$\overline{x}=\frac{430000}{5000}=86$(分)。
2. (2)
解:不能判断$B$地考生数学平均分一定比$A$地考生数学平均分高。
举例:设$B$地甲类学校有考生$1000$人,乙类学校有考生$4000$人。
根据加权平均数公式$\overline{y}=\frac{94×1000+82×4000}{1000 + 4000}$。
先计算分子:$94×1000+82×4000=94000+328000 = 422000$。
再计算分母:$1000 + 4000 = 5000$。
则$\overline{y}=\frac{422000}{5000}=84.4$分。
因为$84.4\lt86$,所以不能判断$B$地考生数学平均分一定比$A$地考生数学平均分高。
综上,(1)$A$地考生的数学平均分是$86$分;(2)不能判断,如上述举例。
查看更多完整答案,请扫码查看


