第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
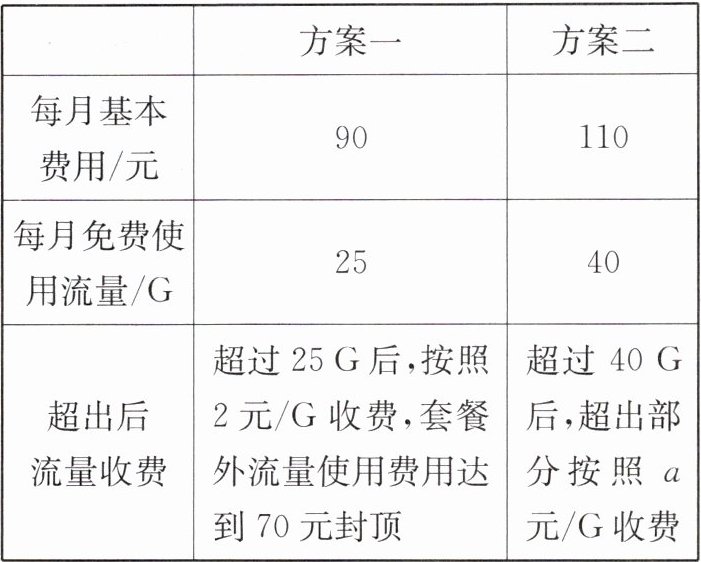
2. 某通信公司就手机流量套餐推出两种方案,如下表:
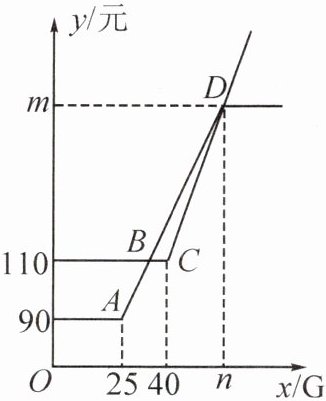
两种方案每月所需费用 y(单位:元)与每月使用流量 x(单位:G)之间的函数图象如图所示。
(1)填空:m =
(2)在方案二中,当每月使用流量超过 40G 时,求每月所需费用 y 与每月使用流量 x 之间的函数表达式。
(3)结合图象,在这两种方案中,当每月使用流量 x 为多少时,选择方案二更划算?请说明理由。

两种方案每月所需费用 y(单位:元)与每月使用流量 x(单位:G)之间的函数图象如图所示。
(1)填空:m =
160
,n =60
,a =2.5
。(2)在方案二中,当每月使用流量超过 40G 时,求每月所需费用 y 与每月使用流量 x 之间的函数表达式。
(3)结合图象,在这两种方案中,当每月使用流量 x 为多少时,选择方案二更划算?请说明理由。

答案:
(1)160 60 2.5
(2)y与x之间的函数表达为$y = \frac{5}{2}x + 10$。
(3)当$35 < x < 60$时,选择方案二更划算。
(1)160 60 2.5
(2)y与x之间的函数表达为$y = \frac{5}{2}x + 10$。
(3)当$35 < x < 60$时,选择方案二更划算。
3. [2024·黑龙江]甲、乙两货车分别从相距 225km 的 A,B 两地同时出发,甲货车从 A 地出发途经配货站时,停下来卸货,半小时后继续驶往 B 地,乙货车沿同一条公路从 B 地驶往 A 地,但乙货车到达配货站时接到紧急任务立即原路原速返回 B 地,结果比甲货车晚半小时到达 B 地。如图是甲、乙两货车距 A 地的距离 y(单位:km)与行驶时间 x(单位:h)之间的函数图象,结合图象回答下列问题:
(1)甲货车到达配货站之前的速度是
(2)求甲货车在配货站卸货后驶往 B 地的过程中,甲货车距 A 地的距离 y 与行驶时间 x 之间的函数表达式;
(3)直接写出甲、乙两货车在行驶的过程中,出发后多长时间甲、乙两货车与配货站的距离相等。
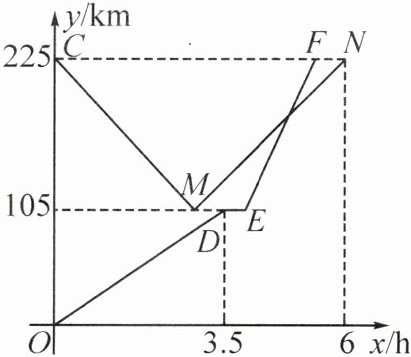
(1)甲货车到达配货站之前的速度是
30
km/h,乙货车的速度是40
km/h;(2)求甲货车在配货站卸货后驶往 B 地的过程中,甲货车距 A 地的距离 y 与行驶时间 x 之间的函数表达式;
(3)直接写出甲、乙两货车在行驶的过程中,出发后多长时间甲、乙两货车与配货站的距离相等。

答案:
(1)30 40
(2)$y = 80x - 215(4\leq x\leq5.5)$
(3)出发后$\frac{3}{2}h$或$\frac{45}{14}h$或$5h$,甲、乙两货车与配货站的距离相等。
(1)30 40
(2)$y = 80x - 215(4\leq x\leq5.5)$
(3)出发后$\frac{3}{2}h$或$\frac{45}{14}h$或$5h$,甲、乙两货车与配货站的距离相等。
查看更多完整答案,请扫码查看


