《2025年全效学习学业评价方案八年级数学上册北师大版》

2. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目：“问有沙田一段，有三斜，其小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三边长分别为 $5$ 里，$12$ 里，$13$ 里，问这块沙田面积有多大？题中的“里”是我国市制长度单位，$1$ 里 $= 500$ 米，则该沙田的面积为(A)

A.$7.5$ 平方千米
B.$15$ 平方千米
C.$75$ 平方千米
D.$750$ 平方千米

答案： 2.A

3. 已知 $a$，$b$，$c$ 是 $\triangle ABC$ 的三边长，且满足关系式 $(c^{2}-a^{2}-b^{2})^{2}+|a - b| = 0$，则 $\triangle ABC$ 的形状为等腰直角三角形。

答案： 3.等腰直角三角形

1. [2024 秋·沈北新区期中]在 $\triangle ABC$ 中，把 $\angle A$，$\angle B$，$\angle C$ 的对边分别记为 $a$，$b$，$c$，由下列条件不能判定 $\triangle ABC$ 为直角三角形的是(D)

A.$\angle A=\angle B-\angle C$
B.$\angle A:\angle B:\angle C = 1:2:3$
C.$a^{2}=c^{2}-b^{2}$
D.$a:b:c = 4:5:6$

答案： 1.D

2. [2024 秋·沈阳期中]当 $n$ 为正整数时，下列各组数：① $3n$，$4n$，$5n$；② $\frac{n}{3}$，$\frac{n}{4}$，$\frac{n}{5}$；③ $2n - 1$，$2n + 1$，$2n + 3$。其中是勾股数的是(A)

A.①
B.①②
C.①③
D.②③

答案： 2.A

3. 如图，$\triangle ABC$ 是等腰三角形，底边 $BC = 20$，$D$ 为 $AB$ 上一点，且 $CD = 16$，$BD = 12$，则 $\triangle ABC$ 的周长为$\frac{160}{3}$。

答案： 3.$\frac{160}{3}$

4. [2024·高唐县期末]图 1 是某品牌婴儿车，图 2 为其简化结构示意图。现测得 $AB = CD = 6\ dm$，$BC = 3\ dm$，$AD = 9\ dm$，其中 $AB$ 与 $BD$ 之间由一个固定为 $90^{\circ}$ 的零件连接（即 $\angle ABD = 90^{\circ}$），根据安全标准需满足 $BC\perp CD$，请通过计算说明该车是否符合安全标准。

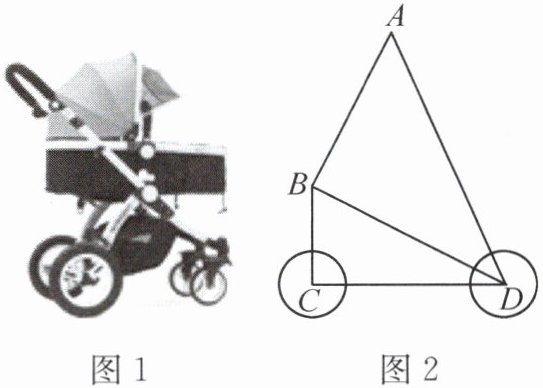
答案： 4.该车符合安全标准。