《2025年全效学习学业评价方案八年级数学上册北师大版》

5. 如图，在正方形 $ABCD$ 中，$E$，$F$ 分别是 $BC$，$CD$ 边上的一点，且 $BE = 2EC$，$FC = \frac{2}{9}DC$，连接 $AE$，$AF$，$EF$，试说明 $\triangle AEF$ 是直角三角形。

答案： 设正方形ABCD的边长为9a。
∵四边形ABCD是正方形，
∴AB=BC=CD=AD=9a，∠B=∠C=∠D=90°。
∵FC=2/9 DC，
∴FC=2/9×9a=2a，DF=DC-FC=9a-2a=7a。
∵BE=2EC，BC=9a，设EC=x，则BE=2x，
∴2x+x=9a，解得x=3a，
∴EC=3a，BE=6a。
在Rt△ABE中，AE²=AB²+BE²=(9a)²+(6a)²=81a²+36a²=117a²。
在Rt△ADF中，AF²=AD²+DF²=(9a)²+(7a)²=81a²+49a²=130a²。
在Rt△ECF中，EF²=EC²+FC²=(3a)²+(2a)²=9a²+4a²=13a²。
∵AE²+EF²=117a²+13a²=130a²=AF²，
∴△AEF是直角三角形。

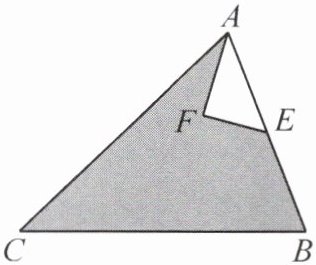
6. [2024·沈阳期中]如图，有一块等腰三角形菜地，其中 $AC = BC = 13\ m$，$AB = 10\ m$，$E$ 为 $AB$ 的中点。现需要开辟一块三角形空地用于堆肥，已知 $AF = 4\ m$，$EF = 3\ m$。
(1)你能确定 $\triangle AEF$ 的形状吗？请说明理由。
(2)计算图中阴影部分的面积。

答案： 1. （1）确定$\triangle AEF$的形状：
解：因为$E$为$AB$的中点，$AB = 10m$，所以$AE=\frac{1}{2}AB = 5m$。
在$\triangle AEF$中，$AF = 4m$，$EF = 3m$，$AE = 5m$。
因为$AF^{2}+EF^{2}=4^{2}+3^{2}=16 + 9=25$，$AE^{2}=5^{2}=25$。
所以$AF^{2}+EF^{2}=AE^{2}$。
根据勾股定理的逆定理：如果三角形的三边长$a$，$b$，$c$满足$a^{2}+b^{2}=c^{2}$，那么这个三角形是直角三角形，其中$c$为斜边。
所以$\triangle AEF$是直角三角形，$\angle AFE = 90^{\circ}$。
2. （2）计算阴影部分的面积：
解：过点$C$作$CD\perp AB$于点$D$。
因为$AC = BC = 13m$，$AB = 10m$，$E$为$AB$中点，$CD\perp AB$，根据等腰三角形三线合一的性质，$AD=\frac{1}{2}AB = 5m$。
在$Rt\triangle ACD$中，根据勾股定理$CD=\sqrt{AC^{2}-AD^{2}}$，已知$AC = 13m$，$AD = 5m$，则$CD=\sqrt{13^{2}-5^{2}}=\sqrt{169 - 25}=\sqrt{144}=12m$。
所以$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD=\frac{1}{2}×10×12 = 60m^{2}$。
又因为$S_{\triangle AEF}=\frac{1}{2}AF\cdot EF=\frac{1}{2}×4×3 = 6m^{2}$。
则阴影部分面积$S = S_{\triangle ABC}-S_{\triangle AEF}$。
所以$S=60 - 6=54m^{2}$。
综上，（1）$\triangle AEF$是直角三角形；（2）阴影部分面积为$54m^{2}$。

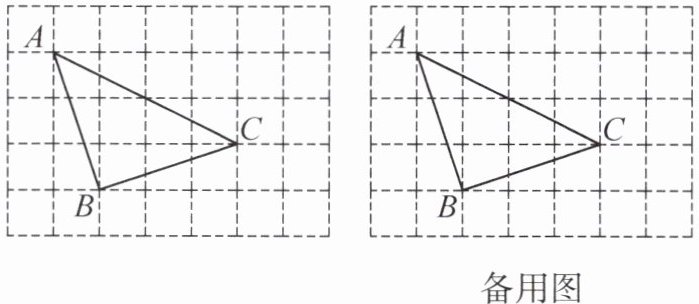
7. (创新意识、模型观念)如图 1，方格纸中的每个小正方形的边长均为 $1$，小正方形的顶点称为格点，已知 $A$，$B$，$C$ 都是格点。
(1)小明发现图中的 $\angle ABC$ 是直角，请补全他的思路；
先利用勾股定理求出 $\triangle ABC$ 的三条边长，可得 $AB^{2}=10$，$BC^{2}=$______①，$AC^{2}=$______②，从而可得 $AB$，$BC$，$AC$ 之间的数量关系是③________，根据④________，可得 $\angle ABC$ 是直角。
(2)请借助备用图用一种不同于小明的方法说明 $\angle ABC$ 是直角。

答案：
1. （1）
计算$BC^{2}$和$AC^{2}$：
根据勾股定理$a^{2}+b^{2}=c^{2}$（其中$a$、$b$为直角边，$c$为斜边），对于$BC$，横向格点数为$3$，纵向格点数为$1$，则$BC^{2}=3^{2}+1^{2}=9 + 1=10$；
对于$AC$，横向格点数为$4$，纵向格点数为$2$，则$AC^{2}=4^{2}+2^{2}=16 + 4=20$。
得出数量关系和定理：
所以$AB^{2}+BC^{2}=10 + 10=20$，$AC^{2}=20$，即$AB^{2}+BC^{2}=AC^{2}$。
根据勾股定理的逆定理（如果三角形的三边长$a$、$b$、$c$满足$a^{2}+b^{2}=c^{2}$，那么这个三角形是直角三角形），可得$\angle ABC$是直角。
故答案依次为：$10$；$20$；$AB^{2}+BC^{2}=AC^{2}$；勾股定理的逆定理。
2. （2）
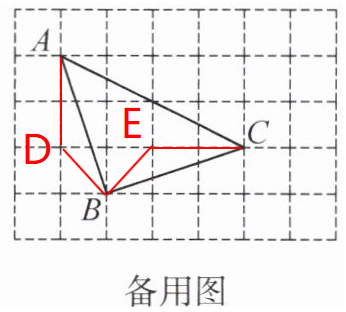
解：
如图，连接$BD$、$BE$（$D$、$E$为格点），$BD=\sqrt{1^{2}+1^{2}}=\sqrt{2}$，$BE=\sqrt{2^{2}+2^{2}}=\sqrt{8}$，$DE=\sqrt{3^{2}+1^{2}}=\sqrt{10}$。
因为$BD^{2}+BE^{2}=(\sqrt{2})^{2}+(\sqrt{8})^{2}=2 + 8=10$，$DE^{2}=(\sqrt{10})^{2}=10$，所以$BD^{2}+BE^{2}=DE^{2}$，$\angle DBE = 90^{\circ}$。
又因为$\triangle ABD\cong\triangle CBE$（$AB = BC=\sqrt{10}$，$BD = BE=\sqrt{2}$，$AD = CE=\sqrt{1^{2}+3^{2}}=\sqrt{10}$，根据$SSS$全等判定），所以$\angle ABD=\angle CBE$。
所以$\angle ABC=\angle ABD+\angle DBC=\angle CBE+\angle DBC = 90^{\circ}$。
（注：方法不唯一，也可以通过构造矩形等方法证明）