《2025年全效学习学业评价方案八年级数学上册北师大版》

例题 韩信率领 1500 名士兵与敌方交战之后，幸存士兵稍多于 1000 名。为了清点幸存士兵的人数，他命令士兵排队。若把幸存士兵按 3 人一排，则多出 2 名；若按 5 人一排，则多出 3 名；若按 7 人一排，则多出 2 名。幸存士兵的人数为(C)

A.1027
B.1037
C.1073
D.1076

答案： 【例】C

1. 一个非负整数 $ a $，它的 30 倍减 2 能被 2024 整除，$ a $ 的最小值是(C)

A.21
B.262
C.135
D.265

答案： 1.C

2. 一个数除以 5 余 2，除以 6 余 2，除以 7 余 3，求能满足这三个条件的最小自然数是122。

答案： 2.122

3. 恰好能被 6，7，8，9 整除的五位数有179个。

答案： 3.179

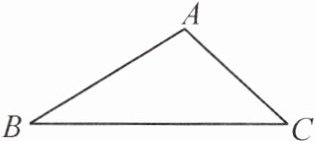
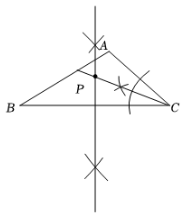
1. 如图，在 $ \triangle ABC $ 中，$ \angle A ＞ 90° $，请用尺规作图的方法在 $ \triangle ABC $ 的内部求作一点 $ P $，使得 $ \triangle PBC $ 是等腰三角形，且点 $ P $ 到边 $ AC $、$ BC $ 的距离相等。（保留作图痕迹，不写作法）

答案：

2. 将分别写有数字 3，7，8 的三张卡片排成三位数 $ \overline{abc} $，使它是 43 的倍数，这个三位数 $ \overline{abc} $ 是387。

答案： 2.387

3. 五位数 $ \overline{A691B} $ 能被 55 整除，这个数最小是46915。

答案： 3.46915

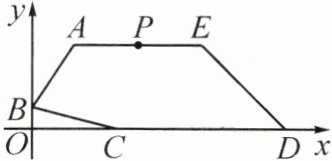
4. （应用意识）如图，在平面直角坐标系中，不规则五边形 $ ABCDE $ 是李大爷家的一块土地的示意图，顶点 $ B $ 在 $ y $ 轴正半轴上，$ CD $ 边在 $ x $ 轴正半轴上，$ AE $ 平行于 $ x $ 轴，$ AE $ 的中点 $ P $ 处有一口灌溉水井。现结合实际耕种需求，需在 $ CD $ 上找一点 $ Q $，使 $ PQ $ 将这块土地的面积分为相等的两部分，用于耕种两种不同的作物，并沿 $ PQ $ 修一条灌溉水渠（水渠的宽度忽略不计）。
（1）请你利用有刻度的直尺在图中画出 $ PQ $ 的位置，并简要说明作图过程；
（2）若点 $ A $ 的坐标为 $ (2,4) $，$ OB = 1 $，$ OC = 4 $，$ OD = 12 $，$ AE = 6 $，请求出直线 $ PQ $ 的函数表达式。

答案： 1. （1）作图过程：
连接$BE$，取$BE$的中点$M$；
连接$PM$并延长交$CD$于点$Q$，则$PQ$即为所求。
理由：因为$AE// x$轴，$P$是$AE$中点，$M$是$BE$中点，根据三角形中位线定理和平行四边形（或梯形）的面积性质，$PQ$能将五边形$ABCDE$的面积分为相等的两部分。
2. （2）
已知$A(2,4)$，$AE = 6$，因为$AE// x$轴，所以$E(2 + 6,4)$，即$E(8,4)$，又$P$是$AE$中点，则$P$点坐标为$(\frac{2 + 8}{2},4)$，即$P(5,4)$。
设直线$BE$的解析式为$y=kx + b$，$B(0,1)$，$E(8,4)$。
把$B(0,1)$，$E(8,4)$代入$y = kx + b$得$\begin{cases}b = 1\\8k + b=4\end{cases}$。
将$b = 1$代入$8k + b = 4$，得$8k+1 = 4$，$8k=3$，解得$k=\frac{3}{8}$。
所以直线$BE$的解析式为$y=\frac{3}{8}x + 1$。
因为$M$是$BE$中点，设$M(x_{M},y_{M})$，根据中点坐标公式$x_{M}=\frac{0 + 8}{2}=4$，$y_{M}=\frac{1 + 4}{2}=\frac{5}{2}$，即$M(4,\frac{5}{2})$。
设直线$PM$的解析式为$y=mx + n$，把$P(5,4)$，$M(4,\frac{5}{2})$代入$y=mx + n$得$\begin{cases}5m + n=4\\4m + n=\frac{5}{2}\end{cases}$。
用$5m + n=4$减去$4m + n=\frac{5}{2}$，得$(5m + n)-(4m + n)=4-\frac{5}{2}$。
即$5m + n - 4m - n=\frac{8 - 5}{2}$，$m=\frac{3}{2}$。
把$m=\frac{3}{2}$代入$5m + n=4$，得$5×\frac{3}{2}+n = 4$，$n=4-\frac{15}{2}=-\frac{7}{2}$。
所以直线$PQ$（即直线$PM$）的函数表达式为$y=\frac{3}{2}x-\frac{7}{2}$。
综上，（1）见上述作图过程；（2）直线$PQ$的函数表达式为$y = \frac{3}{2}x-\frac{7}{2}$。