第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
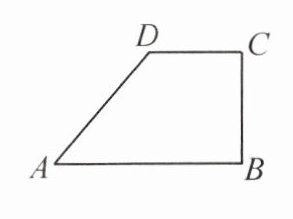
例1 如图,在四边形 $ABCD$ 中,$AB // CD$,$BC \perp AB$,$AD = 5$,$CD = 3$,$BC = 4$。
(1)在原图中建立适当的平面直角坐标系,并写出各顶点的坐标;
(2)在(1)的基础上,分别写出线段 $CD$ 和 $AD$ 上任意一点的坐标。
(1)在原图中建立适当的平面直角坐标系,并写出各顶点的坐标;
(2)在(1)的基础上,分别写出线段 $CD$ 和 $AD$ 上任意一点的坐标。

答案:
(1)以点$A$为原点,$AB$所在直线为$x$轴,建立平面直角坐标系。
(2)线段$CD$上任意一点坐标:$(x, 4)$,其中$3 \leq x \leq 6$。
(1)以点$A$为原点,$AB$所在直线为$x$轴,建立平面直角坐标系。
$\because BC \perp AB$,$CD = 3$,$BC = 4$,$\therefore$点$C$坐标为$(x, 4)$,点$D$坐标为$(x - 3, 4)$($x$为点$B$的横坐标)。
$\because AD = 5$,点$A(0, 0)$,点$D(x - 3, 4)$,$\therefore \sqrt{(x - 3 - 0)^2 + (4 - 0)^2} = 5$,解得$x - 3 = 3$(负值舍去),$\therefore x = 6$。
各顶点坐标:$A(0, 0)$,$B(6, 0)$,$C(6, 4)$,$D(3, 4)$。
(2)线段$CD$上任意一点坐标:$(x, 4)$,其中$3 \leq x \leq 6$。
线段$AD$上任意一点坐标:设$AD$所在直线解析式为$y = kx$,将$D(3, 4)$代入得$k = \frac{4}{3}$,$\therefore y = \frac{4}{3}x$,故坐标为$(x, \frac{4}{3}x)$,其中$0 \leq x \leq 3$。
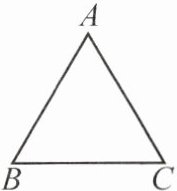
例2 对于边长为 $6$ 的等边三角形 $ABC$。
(1)建立适当的平面直角坐标系,写出各顶点的坐标;
(2)求$\triangle ABC$ 的面积。
(1)建立适当的平面直角坐标系,写出各顶点的坐标;
(2)求$\triangle ABC$ 的面积。

答案:
1. (1)
以$BC$边所在直线为$x$轴,$BC$边的垂直平分线为$y$轴建立平面直角坐标系。
因为$\triangle ABC$是边长为$a = 6$的等边三角形,$BO=CO=\frac{1}{2}BC$,所以$BO = CO=3$。
根据勾股定理$AO=\sqrt{AB^{2}-BO^{2}}$,已知$AB = 6$,$BO = 3$,则$AO=\sqrt{6^{2}-3^{2}}=\sqrt{36 - 9}=\sqrt{27}=3\sqrt{3}$。
所以$A(0,3\sqrt{3})$,$B(-3,0)$,$C(3,0)$。
2. (2)
解:根据三角形面积公式$S=\frac{1}{2}×底×高$。
对于$\triangle ABC$,底$BC = 6$,高$AO = 3\sqrt{3}$。
则$S_{\triangle ABC}=\frac{1}{2}× BC× AO$。
把$BC = 6$,$AO = 3\sqrt{3}$代入公式得$S_{\triangle ABC}=\frac{1}{2}×6×3\sqrt{3}=9\sqrt{3}$。
综上,(1)$A(0,3\sqrt{3})$,$B(-3,0)$,$C(3,0)$;(2)$9\sqrt{3}$。
以$BC$边所在直线为$x$轴,$BC$边的垂直平分线为$y$轴建立平面直角坐标系。
因为$\triangle ABC$是边长为$a = 6$的等边三角形,$BO=CO=\frac{1}{2}BC$,所以$BO = CO=3$。
根据勾股定理$AO=\sqrt{AB^{2}-BO^{2}}$,已知$AB = 6$,$BO = 3$,则$AO=\sqrt{6^{2}-3^{2}}=\sqrt{36 - 9}=\sqrt{27}=3\sqrt{3}$。
所以$A(0,3\sqrt{3})$,$B(-3,0)$,$C(3,0)$。
2. (2)
解:根据三角形面积公式$S=\frac{1}{2}×底×高$。
对于$\triangle ABC$,底$BC = 6$,高$AO = 3\sqrt{3}$。
则$S_{\triangle ABC}=\frac{1}{2}× BC× AO$。
把$BC = 6$,$AO = 3\sqrt{3}$代入公式得$S_{\triangle ABC}=\frac{1}{2}×6×3\sqrt{3}=9\sqrt{3}$。
综上,(1)$A(0,3\sqrt{3})$,$B(-3,0)$,$C(3,0)$;(2)$9\sqrt{3}$。
例3 [2024春·长沙期中]如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系以正东方向为 $x$ 轴的正方向,以正北方向为 $y$ 轴的正方向,并且综合楼和教学楼的坐标分别是$(-4,-1)$和$(1,2)$,那么食堂的坐标是(

A.$(3,5)$
B.$(-2,3)$
C.$(2,4)$
D.$(-1,2)$
B
)
A.$(3,5)$
B.$(-2,3)$
C.$(2,4)$
D.$(-1,2)$
答案:
【例3】B
1. [2023·自贡]如图,边长为 $3$ 的正方形 $OBCD$ 两边与坐标轴正半轴重合,则点 $C$ 的坐标是(
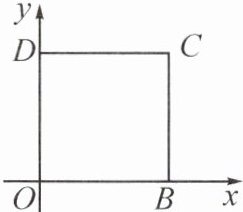
A.$(3,-3)$
B.$(-3,3)$
C.$(3,3)$
D.$(-3,-3)$
C
)
A.$(3,-3)$
B.$(-3,3)$
C.$(3,3)$
D.$(-3,-3)$
答案:
1.C
2. [2024春·沈阳期末]围棋起源于中国古代,是世界上最古老的棋类游戏之一。如图是某围棋棋盘的局部示意图,若棋盘是由边长均为 $1$ 的小正方形组成的,棋盘上 $A$,$B$ 两颗棋子的坐标分别为 $A(-2,4)$,$B(1,2)$,则棋子 $D$ 的坐标为(
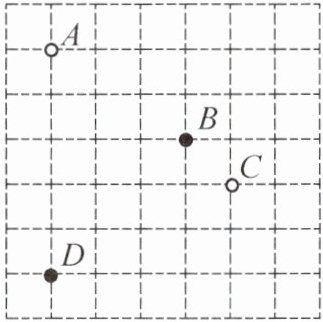
A.$(2,2)$
B.$(-1,-2)$
C.$(-2,-1)$
D.$(2,1)$
C
)
A.$(2,2)$
B.$(-1,-2)$
C.$(-2,-1)$
D.$(2,1)$
答案:
2.C
查看更多完整答案,请扫码查看


