《2025年全效学习学业评价方案八年级数学上册北师大版》

1. 下列说法正确的是(D)

A.$ 4 $ 的算术平方根是 $ 16 $
B.$ -16 $ 的算术平方根是 $ -4 $
C.因为$(-5)^{2}=25$，所以 $ 25 $ 的算术平方根是 $ -5 $
D.$ 1 $ 的算术平方根是 $ 1 $

答案： 1.D

2. 设 $ x $ 是 $ 16 $ 的算术平方根，$ y=(-2)^{2} $，则 $ x $与 $ y $ 的关系是(B)

A.$ x=\pm y $
B.$ x=y $
C.$ x=-y $
D.$ x\neq y $

答案： 2.B

3. [2024 秋·榆阳区校级期中]电流通过导线时会产生热量，电流 $ I $(单位：$ A $)、导线电阻 $ R $(单位：$ \Omega $)、通电时间 $ t $(单位：$ s $)与产生的热量 $ Q $(单位：$ J $)满足 $ Q=I^{2}Rt $。已知导线的电阻为 $ 10 \Omega $，通电后 $ 1 s $ 时间内导线产生 $ 1000 J $ 的热量，电流 $ I $ 的值是(D)

A.$ 2 $
B.$ 5 $
C.$ 8 $
D.$ 10 $

答案： 3.D

4. [2024·广东]完全相同的 $ 4 $ 个正方形面积之和是 $ 100 $，则正方形的边长是5。

答案： 4.5

5. 求下列各式的值：
（1）$\sqrt{81}$；（2）$\sqrt{\frac{144}{289}}$；（3）$\sqrt{1000000}$。

答案： 5.（1）9 （2）$\frac{12}{17}$ （3）1000

6. 计算：
（1）$(\sqrt{6})^{2}+2×(-3)$；
（2）$\sqrt{9}+|-5|-2^{2}$。

答案： 6.（1）0 （2）4

7. 实数 $ a,b $ 在数轴上对应的点的位置如图所示，化简：$\sqrt{a^{2}}-\sqrt{b^{2}}-\sqrt{(a - b)^{2}}+|a + b|$。

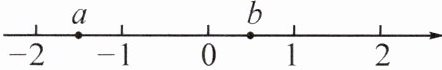
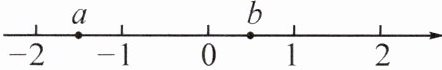
答案： 7.原式=-a-3b。

8. 已知 $ 9 $ 的算术平方根为 $ a $，$|b|=4$，求 $ a - b $ 的值。

答案： 8.a-b的值是-1或7。

9. （应用意识）现有一张长方形绣布，其长、宽之比为 $ 4:3 $，绣布面积为 $ 588 cm^{2} $。
（1）求绣布的周长。
（2）刺绣师傅想利用这张绣布裁出一张面积为 $ 375 cm^{2} $ 的完整圆形绣布来绣花鸟图，她能裁出来吗？请说明理由。（$\pi$取 $ 3 $）

答案： $(1)$ 求绣布的周长
- 步骤一：设未知数并根据面积公式列方程
设长方形绣布的长为$4x cm$，宽为$3x cm$。
根据长方形面积公式$S = 长×宽$，已知绣布面积为$588cm^{2}$，可列方程$4x\cdot3x = 588$。
- 步骤二：解方程求出$x$的值
化简方程$4x\cdot3x = 588$得$12x^{2}=588$，两边同时除以$12$：$x^{2}=\frac{588}{12} = 49$。
因为$x\gt0$，所以$x=\sqrt{49}=7$。
- 步骤三：求出长方形的长、宽和周长
长：$4x = 4×7 = 28cm$；宽：$3x = 3×7 = 21cm$。
根据长方形周长公式$C=(a + b)×2$（其中$a$为长，$b$为宽），可得周长$C=(28 + 21)×2=49×2 = 98cm$。
$(2)$ 判断能否裁出圆形绣布
- 步骤一：求出圆形绣布的半径$r$
已知圆形绣布面积$S_{圆}=375cm^{2}$，$\pi = 3$，根据圆的面积公式$S=\pi r^{2}$，可得$3r^{2}=375$。
两边同时除以$3$：$r^{2}=125$，则$r = \sqrt{125}$（$r\gt0$），直径$d = 2r=2\sqrt{125}$。
- 步骤二：比较圆形绣布直径与长方形绣布宽的大小
$2\sqrt{125}=\sqrt{4×125}=\sqrt{500}$，因为$\sqrt{500}\gt\sqrt{441}$（$\sqrt{441}=21$），即圆形绣布的直径大于长方形绣布的宽。
所以，她不能裁出来。
综上，答案依次为：$(1)$ $98cm$；$(2)$ 不能裁出来，理由：圆形绣布的直径大于长方形绣布的宽。