《2025年云南省标准教辅优佳学案七年级数学上册人教版》

1.计算$1 - 3$,结果是(B).
A.2
B.$-2$
C.4
D.$-4$

答案： 解：根据有理数的减法法则，减去一个数等于加上这个数的相反数。
$1 - 3 = 1 + (-3) = -2$
答案：B

2.比$-1$小2的数是(D).
A.3
B.1
C.$-2$
D.$-3$

答案： 【解析】：
题目要求找到一个数，这个数比-1小2。根据有理数的减法法则，我们可以将问题转化为求$-1 - 2$的值。
【答案】：
解：
$-1 - 2 = -3$
所以，比-1小2的数是-3。
故选D。

3.下列各式中,计算错误的是(B).
A.$(-9)-6= -15$
B.$(-9)-(-6)= 3$
C.$9 - (-6)= 15$
D.$9-(+6)= 3$

答案： 【解析】：
本题主要考察有理数的减法法则。根据有理数的减法法则，减去一个数等于加上这个数的相反数，我们可以将每个选项中的减法表达式转换为加法表达式，然后检查等式是否成立。
A. $(-9) - 6 = -9 + (-6) = -15$，与选项A中的等式一致，所以A是正确的。
B. $(-9) - (-6) = -9 + 6 = -3$，与选项B中的等式$ (-9)-(-6)= 3$不一致，所以B是错误的。
C. $9 - (-6) = 9 + 6 = 15$，与选项C中的等式一致，所以C是正确的。
D. $9 - (+6) = 9 - 6 = 3$，与选项D中的等式一致，所以D是正确的。
综上所述，计算错误的是选项B。
【答案】：
B

4.昆明冬季里某一天的气温为$-1\ ^\circC～8\ ^\circC$,则这一天的温差是(C).
A.$7\ ^\circC$
B.$-7\ ^\circC$
C.$9\ ^\circC$
D.$-9\ ^\circC$

答案： 解：温差 = 最高气温 - 最低气温 = 8 - (-1) = 8 + 1 = 9(°C)
答案：C

5.计算：
(1)$(-37)-14$； (2)$(-8)-(-4)$；
(3)$0 - 2024$； (4)$3\frac{1}{2}-5\frac{1}{4}$.

答案： 【解析】：
本题主要考查有理数的减法法则，即减去一个数等于加上这个数的相反数。
(1) 对于$(-37)-14$，可以转化为$(-37)+(-14)$，即两个负数相加，结果为两数绝对值之和的负数。
(2) 对于$(-8)-(-4)$，可以转化为$(-8)+4$，即负数与正数相加，结果为两数绝对值之差的负数，或理解为负8加4。
(3) 对于$0-2024$，可以转化为$0+(-2024)$，即0加一个负数，结果为那个负数。
(4) 对于$3\frac{1}{2}-5\frac{1}{4}$，首先转化为加法，即$3\frac{1}{2}+(-\frac{21}{4})$，然后进行通分和加法运算。
【答案】：
(1)
解：
$(-37)-14$
$= (-37)+(-14)$
$= -51$
(2)
解：
$(-8)-(-4)$
$= (-8)+4$
$= -4$
(3)
解：
$0-2024$
$= 0+(-2024)$
$= -2024$
(4)
解：
$3\frac{1}{2}-5\frac{1}{4}$
$= 3\frac{1}{2}+(-\frac{21}{4})$
$= \frac{7}{2}-\frac{21}{4}$
$= \frac{14}{4}-\frac{21}{4}$
$= -\frac{7}{4}$
$= -1\frac{3}{4}$

1.计算$(-3)-2$,结果是(C).
A.$-1$
B.1
C.$-5$
D.5

答案： 解：$(-3)-2$
$=(-3)+(-2)$
$=-5$
答案：C

2.已知m是6的相反数,n比m的相反数小2,则$m - n$等于(C).
A.$-2$
B.2
C.$-10$
D.10

答案： 解：因为m是6的相反数，所以$m = -6$。
m的相反数是$-m = 6$，n比m的相反数小2，所以$n = 6 - 2 = 4$。
则$m - n = -6 - 4 = -10$。
答案：C

3.下列各式中,计算错误的是(C).
A.$(-2)-(-2)= 0$
B.$(-3)-4 - 5= -12$
C.$(-7)-(-3)= -10$
D.$3 - 15= -12$

答案： 【解析】：
本题主要考察有理数的减法法则。需要逐一检查每个选项，找出计算错误的选项。
A. $(-2)-(-2)=0$ ，根据有理数的减法法则，减去一个负数等于加上这个数的绝对值，所以 $(-2)-(-2) = (-2)+2 = 0$，计算正确。
B. $(-3)-4-5=-12$ ，根据有理数的加减法，$(-3)-4-5 = -3-4-5 = -12$，计算正确。
C. $(-7)-(-3)=-10$ ，根据有理数的减法法则，$(-7)-(-3) = (-7)+3 = -4$，但题目中给出的是 $-10$，所以计算错误。
D. $3-15=-12$ ，直接进行减法运算，$3-15 = -12$，计算正确。
综上所述，计算错误的选项是C。
【答案】：
C

(1)$(-2\frac{1}{3})-\frac{1}{3}= (-2\frac{1}{3})+$$(-\frac{1}{3})$$=$$-2\frac{2}{3}$；
(2)$0 - (-2.5)= 0 +$$2.5$$=$$2.5$；
(3)$8 - 2024= 8 +$$(-2024)$$=$$-2016$.

答案：
(1)$(-\frac{1}{3})$；$-2\frac{2}{3}$
(2)$2.5$；$2.5$
(3)$(-2024)$；$-2016$

5.如图,某勘探小组测得点E的海拔为$22\ m$,点F的海拔为$-18\ m$(以海平面为基准),则点E比点F高(D).


A.$4\ m$
B.$30\ m$
C.$14\ m$
D.$40\ m$

答案： 【解析】：
本题主要考察有理数的减法法则在实际问题中的应用。
根据题目，点$E$的海拔为$22m$，点$F$的海拔为$-18m$，要求点$E$比点$F$高多少米，即求两点海拔的差值。
海拔差值 = 点E的海拔 - 点F的海拔
= $22m - (-18m)$
= $22m + 18m$
= $40m$
【答案】：
D. $40m$。

6.为了加强对青少年的消防安全教育,某校邀请当地消防大队到校开展消防安全演练活动.消防队员为全体同学展示云梯消防车高层救援,梯架上的工作斗先上升$16\ m$,再下降$32\ m$,再上升$40\ m$,此时工作斗距离初始位置______$m$.
24

答案： 【解析】：
题目考查了有理数的加减法法则。
首先，工作斗上升$16\ m$，可以表示为$+16\ m$；
然后，工作斗下降$32\ m$，可以表示为$-32\ m$；
最后，工作斗再次上升$40\ m$，可以表示为$+40\ m$。
因此，工作斗的总移动距离是初始位置加上这些移动，即：
$0 + 16 - 32 + 40 = 24 \ (m)$。
【答案】：
$24$

7.有一口水井,水面比井口低$1\ m$,一只蜗牛从水面沿井壁往井口爬,它每天白天向上爬行$32\ cm$,但每天晚上又下滑$20\ cm$.蜗牛爬出井口需要的天数是______7.

答案： 【解析】：
首先，将井的深度和蜗牛每天爬升与下滑的距离都统一到同一单位，即厘米。
井的深度为$1m = 100cm$。
蜗牛每天白天爬升$32cm$，但晚上会下滑$20cm$，所以蜗牛每天的“净爬升”（白天爬升高度减去晚上下滑高度）是$32cm - 20cm = 12cm$。
然后，我们需要考虑蜗牛最后一天爬升的特殊情况：
当蜗牛接近井口时，它实际上可能在白天就能爬出来，而无需再等到晚上滑下去。
假设蜗牛在第$N$天的白天就能爬出井口。那么，第$N-1$天晚上下滑完至少达到了以下高度：
$第(N-1)天下滑后的高度 + 32 \ge 100$
$第(N-1)天下滑后的高度 \ge 68$
考虑每天蜗牛净爬升$12cm$，第6天晚上下滑后才能超过$68cm$的高度，故$N-1=6$，从而$N=7$。
【答案】：
7

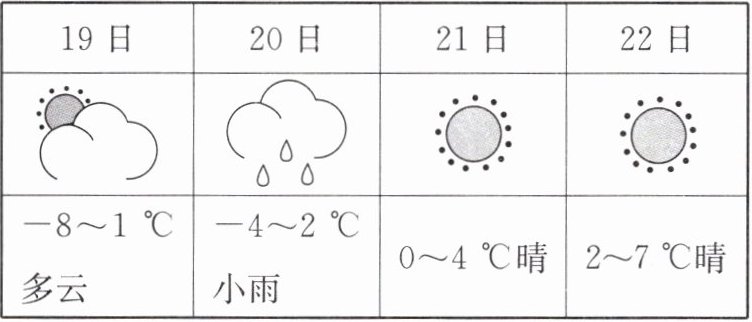
8.某地连续四天的天气情况如下表,其中温差最大的一天是(A).
| 19日 | 20日 | 21日 | 22日 |
| -8~1℃多云 | -4~2℃小雨 | 0~4℃晴 | 2~7℃晴 |


A.19日
B.20日
C.21日
D.22日

答案： 解：19日温差：$1 - (-8) = 1 + 8 = 9℃$
20日温差：$2 - (-4) = 2 + 4 = 6℃$
21日温差：$4 - 0 = 4℃$
22日温差：$7 - 2 = 5℃$
$9℃ ＞ 6℃ ＞ 5℃ ＞ 4℃$，温差最大的是19日。
答案：A