第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
8.(跨学科融合)我国新疆大部分地区有时昼夜温差极大,故历来有“早穿皮袄午穿纱,围着火炉吃西瓜”之说.如果新疆某地某天的最低气温为-5℃,且全天最大温差为30℃,那么当天的最高气温是
25
℃.
答案:
【解析】:
这个问题涉及到有理数的加法运算,特别是涉及温差的计算。
题目给出了最低气温和温差,要求计算最高气温。
根据有理数的加法法则,最高气温 = 最低气温 + 温差。
【答案】:
解:根据题意,最低气温为 $-5^\circ C$,温差为 $30^\circ C$。
所以,最高气温 = 最低气温 + 温差
= $-5^\circ C + 30^\circ C$
= $25^\circ C$。
故答案为:$25^\circ C$。
这个问题涉及到有理数的加法运算,特别是涉及温差的计算。
题目给出了最低气温和温差,要求计算最高气温。
根据有理数的加法法则,最高气温 = 最低气温 + 温差。
【答案】:
解:根据题意,最低气温为 $-5^\circ C$,温差为 $30^\circ C$。
所以,最高气温 = 最低气温 + 温差
= $-5^\circ C + 30^\circ C$
= $25^\circ C$。
故答案为:$25^\circ C$。
9.《九章算术》中用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数,白色为正,黑色为负.如图(1)表示的是(+21)+(-32)= -11的计算过程,则图(2)表示的计算过程是
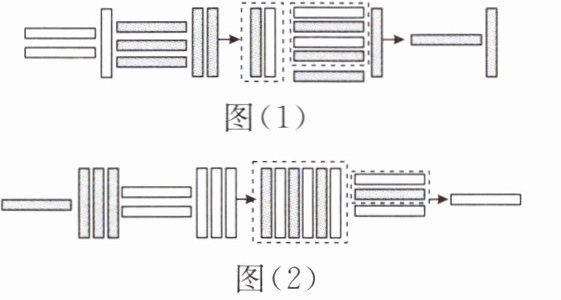
(-13)+(+23)=10
.
答案:
解:(-13)+(+23)=10
10.下表列出了国外两个城市与北京的时差(负号表示同一时刻,巴黎时间比北京时间晚).如果现在北京时间是10:00,那么现在巴黎时间是
|城市|时差/h|
|巴黎|-7|
|东京|+1|

3:00
.|城市|时差/h|
|巴黎|-7|
|东京|+1|

答案:
【解析】:
题目考查有理数的加法法则,特别是涉及带负数的加法运算。
题目给出了巴黎与北京的时差是$-7$小时,这意味着巴黎时间比北京时间晚$7$小时。
现在北京时间是$10:00$,需要计算巴黎的时间。
根据时差,巴黎时间 = 北京时间 + 时差 = $10:00 + (-7)$小时。
进行加法运算,得出巴黎时间。
【答案】:
巴黎时间 = $10:00 + (-7小时) = 3:00$。
故答案为$3:00$。
题目考查有理数的加法法则,特别是涉及带负数的加法运算。
题目给出了巴黎与北京的时差是$-7$小时,这意味着巴黎时间比北京时间晚$7$小时。
现在北京时间是$10:00$,需要计算巴黎的时间。
根据时差,巴黎时间 = 北京时间 + 时差 = $10:00 + (-7)$小时。
进行加法运算,得出巴黎时间。
【答案】:
巴黎时间 = $10:00 + (-7小时) = 3:00$。
故答案为$3:00$。
11.若两个数的和为负数,则这两个数一定(
A.同正
B.同负
C.一正一负
D.至少有一个负数
D
).A.同正
B.同负
C.一正一负
D.至少有一个负数
答案:
【解析】:
这个问题考查的是有理数的加法法则。根据有理数的加法法则,如果两个数的和为负数,那么这两个数中至少有一个是负数。具体分析如下:
A选项:若两数同为正数,则和为正数,与题目给定的和为负数矛盾,故A错误。
B选项:若两数同为负数,则和确实为负数,但这并不是唯一情况,因为一正一负(且负数的绝对值大于正数)的情况下和也可能为负数,故B虽然可能正确但不是唯一正确答案。
C选项:一正一负的情况下,和的正负取决于绝对值较大的那个数,如果负数的绝对值大于正数,则和为负数,但反之亦然。因此,C不是必然正确。
D选项:无论其他数的具体情况如何,只要两个数的和为负数,那么这两个数中至少有一个是负数。这是唯一必然正确的选项。
【答案】:
D.至少有一个负数。
这个问题考查的是有理数的加法法则。根据有理数的加法法则,如果两个数的和为负数,那么这两个数中至少有一个是负数。具体分析如下:
A选项:若两数同为正数,则和为正数,与题目给定的和为负数矛盾,故A错误。
B选项:若两数同为负数,则和确实为负数,但这并不是唯一情况,因为一正一负(且负数的绝对值大于正数)的情况下和也可能为负数,故B虽然可能正确但不是唯一正确答案。
C选项:一正一负的情况下,和的正负取决于绝对值较大的那个数,如果负数的绝对值大于正数,则和为负数,但反之亦然。因此,C不是必然正确。
D选项:无论其他数的具体情况如何,只要两个数的和为负数,那么这两个数中至少有一个是负数。这是唯一必然正确的选项。
【答案】:
D.至少有一个负数。
12.小邱同学遇到这样一道题:计算|(-6)+■|.其中“■”是被墨水污染看不清的一个数,他翻看了后面的答案,得知该题的答案是15,那么“■”表示的数是(
A.9
B.9或-21
C.-21
D.-9或21
D
).A.9
B.9或-21
C.-21
D.-9或21
答案:
解:设“■”表示的数是$x$,则$|(-6) + x| = 15$。
根据绝对值的性质,得$-6 + x = 15$或$-6 + x = -15$。
当$-6 + x = 15$时,$x = 15 + 6 = 21$;
当$-6 + x = -15$时,$x = -15 + 6 = -9$。
所以“■”表示的数是$-9$或$21$。
答案:D
根据绝对值的性质,得$-6 + x = 15$或$-6 + x = -15$。
当$-6 + x = 15$时,$x = 15 + 6 = 21$;
当$-6 + x = -15$时,$x = -15 + 6 = -9$。
所以“■”表示的数是$-9$或$21$。
答案:D
13.若|m|= 2,|n|= 3,m<0,n>0,则m+n的值为(
A.6
B.1
C.-1
D.-6
B
).A.6
B.1
C.-1
D.-6
答案:
解:
∵|m|=2,m<0,
∴m=-2.
∵|n|=3,n>0,
∴n=3.
∴m+n=-2+3=1.
答案:B
∵|m|=2,m<0,
∴m=-2.
∵|n|=3,n>0,
∴n=3.
∴m+n=-2+3=1.
答案:B
14.(1)已知|a+8|+|b-4|= 0,则a+|b|的值是
(2)(易错题)一个数是8,另一个数比8的相反数大-2,则这两个数的和为
-4
;(2)(易错题)一个数是8,另一个数比8的相反数大-2,则这两个数的和为
-2
.
答案:
(1)解:因为|a+8|≥0,|b-4|≥0,且|a+8|+|b-4|=0,所以a+8=0,b-4=0,解得a=-8,b=4。则a+|b|=-8+|4|=-8+4=-4。
(2)解:8的相反数是-8,另一个数比-8大-2,即-8+(-2)=-10。这两个数的和为8+(-10)=-2。
(1)解:因为|a+8|≥0,|b-4|≥0,且|a+8|+|b-4|=0,所以a+8=0,b-4=0,解得a=-8,b=4。则a+|b|=-8+|4|=-8+4=-4。
(2)解:8的相反数是-8,另一个数比-8大-2,即-8+(-2)=-10。这两个数的和为8+(-10)=-2。
15.列式计算:
(1)已知两个数是$5\frac{5}{6}和-8\frac{2}{3}$,则这两个数的和是多少?
(2)什么数与$-\frac{5}{12}的差等于-\frac{7}{8}$?
(1)已知两个数是$5\frac{5}{6}和-8\frac{2}{3}$,则这两个数的和是多少?
(2)什么数与$-\frac{5}{12}的差等于-\frac{7}{8}$?
答案:
【解析】:
本题主要考查有理数的加法法则以及列式计算的能力。
(1) 对于第一问,需要计算两个有理数 $5\frac{5}{6}$ 和 $-8\frac{2}{3}$ 的和。
根据有理数的加法法则,同号数相加取相同的符号,异号数相加取绝对值之差的符号,并用较大的绝对值减去较小的绝对值。
但在这里,我们直接进行加法运算,注意负数的处理。
(2) 对于第二问,需要找到一个数,使其与 $-\frac{5}{12}$ 的差等于 $-\frac{7}{8}$。
设这个数为 $x$,则可以列出方程 $x - (-\frac{5}{12}) = -\frac{7}{8}$,
即 $x + \frac{5}{12} = -\frac{7}{8}$,
解这个方程即可求出 $x$ 的值。
【答案】:
(1) 解:
$5\frac{5}{6} + (-8\frac{2}{3})$
$= \frac{35}{6} - \frac{26}{3}$
$= \frac{35}{6} - \frac{52}{6}$
$= -\frac{17}{6}$
$= -2\frac{5}{6}$
(2) 解:
设这个数为 $x$,
则 $x - (-\frac{5}{12}) = -\frac{7}{8}$,
即 $x + \frac{5}{12} = -\frac{7}{8}$,
$x = -\frac{7}{8} - \frac{5}{12}$
$= -\frac{21}{24} - \frac{10}{24}$
$= -\frac{31}{24}$
$= -1\frac{7}{24}$
本题主要考查有理数的加法法则以及列式计算的能力。
(1) 对于第一问,需要计算两个有理数 $5\frac{5}{6}$ 和 $-8\frac{2}{3}$ 的和。
根据有理数的加法法则,同号数相加取相同的符号,异号数相加取绝对值之差的符号,并用较大的绝对值减去较小的绝对值。
但在这里,我们直接进行加法运算,注意负数的处理。
(2) 对于第二问,需要找到一个数,使其与 $-\frac{5}{12}$ 的差等于 $-\frac{7}{8}$。
设这个数为 $x$,则可以列出方程 $x - (-\frac{5}{12}) = -\frac{7}{8}$,
即 $x + \frac{5}{12} = -\frac{7}{8}$,
解这个方程即可求出 $x$ 的值。
【答案】:
(1) 解:
$5\frac{5}{6} + (-8\frac{2}{3})$
$= \frac{35}{6} - \frac{26}{3}$
$= \frac{35}{6} - \frac{52}{6}$
$= -\frac{17}{6}$
$= -2\frac{5}{6}$
(2) 解:
设这个数为 $x$,
则 $x - (-\frac{5}{12}) = -\frac{7}{8}$,
即 $x + \frac{5}{12} = -\frac{7}{8}$,
$x = -\frac{7}{8} - \frac{5}{12}$
$= -\frac{21}{24} - \frac{10}{24}$
$= -\frac{31}{24}$
$= -1\frac{7}{24}$
16.有3筐白菜,以每筐25 kg为质量标准,超过或不足的千克数分别用正数、负数来表示,称后的记录(单位:kg)如下:-1.5,0,+1.
(1)分别求出这3筐白菜的质量;
(2)3筐白菜总计超过多少千克或不足多少千克?
(1)分别求出这3筐白菜的质量;
(2)3筐白菜总计超过多少千克或不足多少千克?
答案:
(1)解:第一筐:25 + (-1.5) = 23.5(kg)
第二筐:25 + 0 = 25(kg)
第三筐:25 + 1 = 26(kg)
答:这3筐白菜的质量分别为23.5kg,25kg,26kg。
(2)解:(-1.5) + 0 + 1 = -0.5(kg)
答:3筐白菜总计不足0.5千克。
(1)解:第一筐:25 + (-1.5) = 23.5(kg)
第二筐:25 + 0 = 25(kg)
第三筐:25 + 1 = 26(kg)
答:这3筐白菜的质量分别为23.5kg,25kg,26kg。
(2)解:(-1.5) + 0 + 1 = -0.5(kg)
答:3筐白菜总计不足0.5千克。
17.(运算能力)(1)用“>”“<”或“=”填空:
|(-3)+(-5)|
|6+(-2)|
|(-8)+5|
|(-7)+0|
(2)归纳猜想:|a+b|
|(-3)+(-5)|
=
|-3|+|-5|,|6+(-2)|
<
|6|+|-2|,|(-8)+5|
<
|-8|+|5|,|(-7)+0|
=
|-7|+|0|;(2)归纳猜想:|a+b|
≤
|a|+|b|.
答案:
【解析】:
本题主要考察了有理数的加法法则以及绝对值的性质。
首先,我们计算各个具体的表达式:
1. $|(-3)+(-5)| = |-8| = 8$,而 $|-3| + |-5| = 3 + 5 = 8$,所以 $|(-3)+(-5)| = |-3| + |-5|$;
2. $|6+(-2)| = |4| = 4$,而 $|6| + |-2| = 6 + 2 = 8$,所以 $|6+(-2)| < |6| + |-2|$;
3. $|(-8)+5| = |-3| = 3$,而 $|-8| + |5| = 8 + 5 = 13$,所以 $|(-8)+5| < |-8| + |5|$;
4. $|(-7)+0| = |-7| = 7$,而 $|-7| + |0| = 7 + 0 = 7$,所以 $|(-7)+0| = |-7| + |0|$。
通过观察这些具体的例子,我们可以归纳出 $|a+b|$ 和 $|a| + |b|$ 之间的关系。
当 $a$ 和 $b$ 同号时,$|a+b| = |a| + |b|$;
当 $a$ 和 $b$ 异号时,$|a+b| < |a| + |b|$;
当 $a$ 和 $b$ 中至少有一个为0时,$|a+b| = |a| + |b|$。
综合以上三种情况,我们可以得出 $|a+b| \leq |a| + |b|$。
【答案】:
(1) $=$,$<$,$<$,$=$
(2) $|a+b| \leq |a| + |b|$
本题主要考察了有理数的加法法则以及绝对值的性质。
首先,我们计算各个具体的表达式:
1. $|(-3)+(-5)| = |-8| = 8$,而 $|-3| + |-5| = 3 + 5 = 8$,所以 $|(-3)+(-5)| = |-3| + |-5|$;
2. $|6+(-2)| = |4| = 4$,而 $|6| + |-2| = 6 + 2 = 8$,所以 $|6+(-2)| < |6| + |-2|$;
3. $|(-8)+5| = |-3| = 3$,而 $|-8| + |5| = 8 + 5 = 13$,所以 $|(-8)+5| < |-8| + |5|$;
4. $|(-7)+0| = |-7| = 7$,而 $|-7| + |0| = 7 + 0 = 7$,所以 $|(-7)+0| = |-7| + |0|$。
通过观察这些具体的例子,我们可以归纳出 $|a+b|$ 和 $|a| + |b|$ 之间的关系。
当 $a$ 和 $b$ 同号时,$|a+b| = |a| + |b|$;
当 $a$ 和 $b$ 异号时,$|a+b| < |a| + |b|$;
当 $a$ 和 $b$ 中至少有一个为0时,$|a+b| = |a| + |b|$。
综合以上三种情况,我们可以得出 $|a+b| \leq |a| + |b|$。
【答案】:
(1) $=$,$<$,$<$,$=$
(2) $|a+b| \leq |a| + |b|$
查看更多完整答案,请扫码查看


