第162页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
【例1】在日常生活中,我们一拧水龙头,水就源源不断地流出来,可能丝毫感觉不到因浪费水而导致的危机.但事实上,我国是一个缺水国家,我们赖以生存的水,正日益短缺.节约用水,是我们每一个公民的基本素养之一.为鼓励居民节约用水,某市对居民用水收费实行“阶梯价”,2022年起年具体收费标准如下表(阶梯价的含义:年用水量不超过$144\ m^3$,每立方米收费$3.15$元,年用水量在$144~240\ m^3$,前$144\ m^3按3.15\ 元/m^3$收费,在$144~240\ m^3之间的用水量按4.05\ 元/m^3$收费,依此类推).
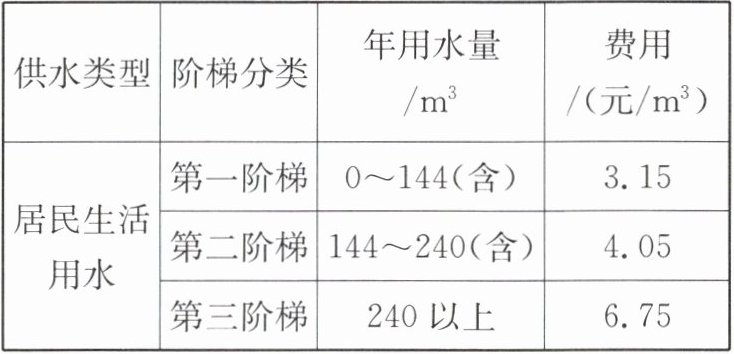
(1)设某户居民的年用水量为$t\ m^3$($t$是正整数),请你列表说明,当$t$在不同范围内取值时,如何计费?
(2)若小红家2023年全年用水量为$120\ m^3$,则小红家应缴水费______元.
(3)若小明家2023年缴水费441元,求小明家2023年全年用水量.(列方程解决问题)
(4)若小刚家2023年缴水费575.1元,求小刚家2023年全年用水量.(列方程解决问题)

(1)设某户居民的年用水量为$t\ m^3$($t$是正整数),请你列表说明,当$t$在不同范围内取值时,如何计费?
(2)若小红家2023年全年用水量为$120\ m^3$,则小红家应缴水费______元.
(3)若小明家2023年缴水费441元,求小明家2023年全年用水量.(列方程解决问题)
(4)若小刚家2023年缴水费575.1元,求小刚家2023年全年用水量.(列方程解决问题)
答案:
【解析】:本题主要考察分段计费问题的理解和应用。
(1) 设每户每月用水量为$t$立方米,应缴水费为$y$元。根据题目条件,我们可以列出以下分段函数关系:当$0 \leq t \leq 200$时,$y = 1.9t$(基础水费);当$t > 200$时,$y = 2.85(t - 200) + 1.9 × 200$(超出部分加价水费)。
(2) 小红家2023年全年用水量为$120m^3$,由于$120 \leq 200$,所以应用基础水费公式计算:$y = 1.9 × 120 = 228$元。
(3) 小明家2023年缴水费441元,由于$441 > 1.9 × 200 = 380$,所以小明家的用水量一定超过了200立方米。设小明家全年用水量为$x$立方米,则可以列出方程:$2.85(x - 200) + 1.9 × 200 = 441$解这个方程,我们得到:$2.85x - 570 + 380 = 441$$2.85x = 631$$x = 220$所以,小明家2023年全年用水量为220立方米。
(4) 小刚家2023年缴水费575.1元,由于$575.1 > 1.9 × 200 = 380$,所以小刚家的用水量也超过了200立方米。设小刚家全年用水量为$a$立方米,则可以列出方程:$2.85(a - 200) + 1.9 × 200 = 575.1$解这个方程,我们得到:$2.85a - 570 + 380 = 575.1$$2.85a = 765.1$$a \approx 268.46$(结果保留两位小数)所以,小刚家2023年全年用水量约为268.46立方米。【答案】:
(1) 当$0 \leq t \leq 200$时,$y = 1.9t$;当$t > 200$时,$y = 2.85(t - 200) + 380$。
(2) 228元。
(3) 小明家2023年全年用水量为220立方米。
(4) 小刚家2023年全年用水量约为268.46立方米。
(1) 设每户每月用水量为$t$立方米,应缴水费为$y$元。根据题目条件,我们可以列出以下分段函数关系:当$0 \leq t \leq 200$时,$y = 1.9t$(基础水费);当$t > 200$时,$y = 2.85(t - 200) + 1.9 × 200$(超出部分加价水费)。
(2) 小红家2023年全年用水量为$120m^3$,由于$120 \leq 200$,所以应用基础水费公式计算:$y = 1.9 × 120 = 228$元。
(3) 小明家2023年缴水费441元,由于$441 > 1.9 × 200 = 380$,所以小明家的用水量一定超过了200立方米。设小明家全年用水量为$x$立方米,则可以列出方程:$2.85(x - 200) + 1.9 × 200 = 441$解这个方程,我们得到:$2.85x - 570 + 380 = 441$$2.85x = 631$$x = 220$所以,小明家2023年全年用水量为220立方米。
(4) 小刚家2023年缴水费575.1元,由于$575.1 > 1.9 × 200 = 380$,所以小刚家的用水量也超过了200立方米。设小刚家全年用水量为$a$立方米,则可以列出方程:$2.85(a - 200) + 1.9 × 200 = 575.1$解这个方程,我们得到:$2.85a - 570 + 380 = 575.1$$2.85a = 765.1$$a \approx 268.46$(结果保留两位小数)所以,小刚家2023年全年用水量约为268.46立方米。【答案】:
(1) 当$0 \leq t \leq 200$时,$y = 1.9t$;当$t > 200$时,$y = 2.85(t - 200) + 380$。
(2) 228元。
(3) 小明家2023年全年用水量为220立方米。
(4) 小刚家2023年全年用水量约为268.46立方米。
【例2】实验与探究:小明学完一元一次方程后,用一根质地均匀60 cm长的木杆和一些等重的小物体,做如图(1)所示的实验:
①在木杆正中间处拴绳,将木杆吊起并使其左右平衡,吊绳处为木杆的支点;
②在木杆两端各悬挂一重物,看看左右是否保持平衡;
③小明在木杆左端小物体下加挂一重物,然后把这两个重物一起向右移动,直至左右平衡,记录此时支点到木杆左右两边挂重物处的距离;
④在木杆左端两小物体下继续加挂重物,并重复以上操作.
记录情况如下表所示.
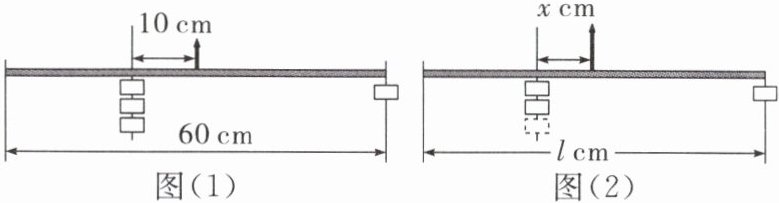
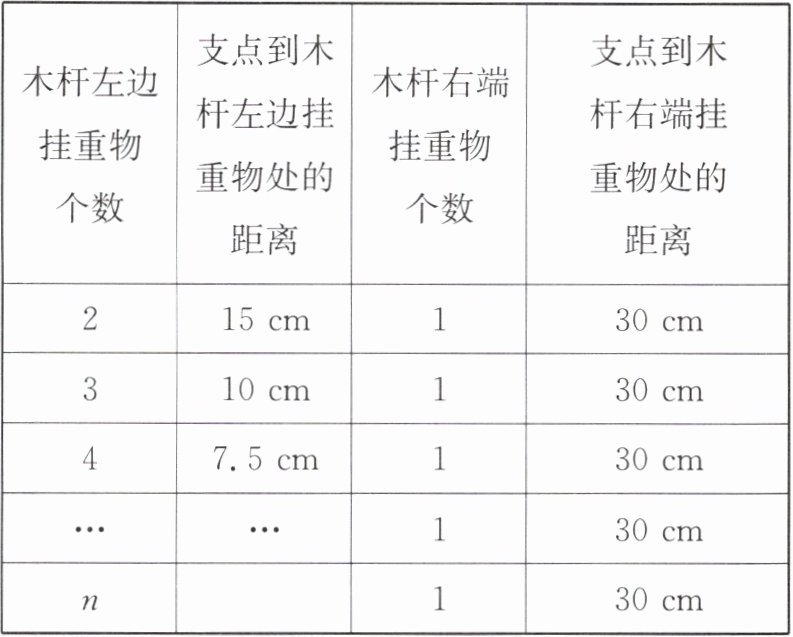
(1)根据以上小明的记录你能发现什么规律?能否用语言进行表述?
(2)如图(2),在木杆右端挂一重物,支点左边挂$n$个重物,并使左右平衡.设木杆长为$l\ cm$,支点到木杆左边挂重物处的距离为$x\ cm$,把$n,l$作为已知数,列出关于$x$的一元一次方程.
①在木杆正中间处拴绳,将木杆吊起并使其左右平衡,吊绳处为木杆的支点;
②在木杆两端各悬挂一重物,看看左右是否保持平衡;
③小明在木杆左端小物体下加挂一重物,然后把这两个重物一起向右移动,直至左右平衡,记录此时支点到木杆左右两边挂重物处的距离;
④在木杆左端两小物体下继续加挂重物,并重复以上操作.
记录情况如下表所示.


(1)根据以上小明的记录你能发现什么规律?能否用语言进行表述?
(2)如图(2),在木杆右端挂一重物,支点左边挂$n$个重物,并使左右平衡.设木杆长为$l\ cm$,支点到木杆左边挂重物处的距离为$x\ cm$,把$n,l$作为已知数,列出关于$x$的一元一次方程.
答案:
【解析】:
(1) 通过观察小明的记录,我们可以发现杠杆平衡的规律,即力矩(力×力臂)的平衡原理。在这个问题中,当木杆达到平衡状态时,左边的力矩总和等于右边的力矩。这个规律可以用语言表述为:当木杆达到平衡时,各力对其支点的力矩之和为零,也就是说,动力×动力臂=阻力×阻力臂。
(2) 对于第二个问题,我们首先需要理解杠杆平衡的原理,然后利用这个原理来列出关于$x$的一元一次方程。设木杆右端挂的重物产生的力矩为$M_2$,支点左边每个重物产生的力矩为$M_1$,则有$n$个$M_1$(因为有$n$个重物),根据力矩平衡原理,我们有$nM_1 = M_2$。假设每个重物的重量都相同,那么力矩就与力臂的长度成正比,因此我们可以将这个关系转化为关于$x$的一元一次方程。设木杆右端挂的重物到支点的距离为$(l-x)$,则根据力矩平衡,我们可以列出方程:$n × x = (l - x) × 1$(这里假设每个重物的重量为1单位重量,因此力矩就等于力臂的长度)。简化后得到:$nx = l - x$,进一步整理得到:$(n+1)x = l$。【答案】:
(1) 能发现杠杆平衡的规律,即当木杆达到平衡状态时,左边的力矩总和等于右边的力矩。
(2) 关于$x$的一元一次方程为:$(n+1)x = l$。
(1) 通过观察小明的记录,我们可以发现杠杆平衡的规律,即力矩(力×力臂)的平衡原理。在这个问题中,当木杆达到平衡状态时,左边的力矩总和等于右边的力矩。这个规律可以用语言表述为:当木杆达到平衡时,各力对其支点的力矩之和为零,也就是说,动力×动力臂=阻力×阻力臂。
(2) 对于第二个问题,我们首先需要理解杠杆平衡的原理,然后利用这个原理来列出关于$x$的一元一次方程。设木杆右端挂的重物产生的力矩为$M_2$,支点左边每个重物产生的力矩为$M_1$,则有$n$个$M_1$(因为有$n$个重物),根据力矩平衡原理,我们有$nM_1 = M_2$。假设每个重物的重量都相同,那么力矩就与力臂的长度成正比,因此我们可以将这个关系转化为关于$x$的一元一次方程。设木杆右端挂的重物到支点的距离为$(l-x)$,则根据力矩平衡,我们可以列出方程:$n × x = (l - x) × 1$(这里假设每个重物的重量为1单位重量,因此力矩就等于力臂的长度)。简化后得到:$nx = l - x$,进一步整理得到:$(n+1)x = l$。【答案】:
(1) 能发现杠杆平衡的规律,即当木杆达到平衡状态时,左边的力矩总和等于右边的力矩。
(2) 关于$x$的一元一次方程为:$(n+1)x = l$。
查看更多完整答案,请扫码查看


