《2025年云南省标准教辅优佳学案七年级数学上册人教版》

1. 给定一列按规律排列的数：1,$\frac{1}{3}$,$\frac{1}{5}$,$\frac{1}{7}$,$\frac{1}{9}$,…,它的第10个数是( ).

A.$\frac{1}{15}$
B.$\frac{1}{17}$
C.$\frac{1}{19}$
D.$\frac{1}{21}$

答案： 解：观察这列数：1，$\frac{1}{3}$，$\frac{1}{5}$，$\frac{1}{7}$，$\frac{1}{9}$，…，可写成$\frac{1}{1}$，$\frac{1}{3}$，$\frac{1}{5}$，$\frac{1}{7}$，$\frac{1}{9}$，…。
分子均为1，分母依次为1，3，5，7，9，…，是从1开始的连续奇数，其规律为第n个数的分母是$2n - 1$。
当$n = 10$时，分母为$2×10 - 1 = 19$，所以第10个数是$\frac{1}{19}$。
答案：C

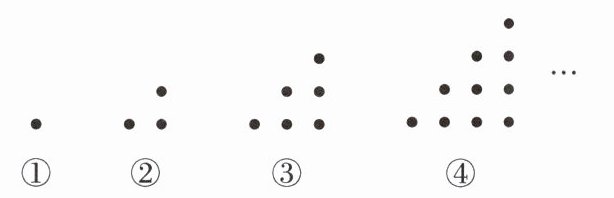
2. 把黑色棋子按如图所示的规律拼图案,其中第①个图案中有1颗棋子,第②个图案中有3颗棋子,第③个图案中有6颗棋子……按此规律排列下去,则第⑥个图案中棋子的颗数为( ).


A.19
B.21
C.23
D.25

答案： 【解析】：
这个问题主要考查的是数列求和的规律识别与运用。
首先，观察图案中棋子的数量，可以看到它们构成了一个特定的数列：1，3，6，...。
第①个图案：1颗棋子，可以表示为1；
第②个图案：比第①个多2颗，共3颗，即1+2；
第③个图案：比第②个多3颗，共6颗，即1+2+3；
以此类推，可以发现第n个图案中的棋子数量是前n个自然数的和，即$1 + 2 + 3 + ... + n$。
这是一个等差数列的求和问题，其和公式为$\frac{n(n + 1)}{2}$。
接下来，应用这个公式来找出第⑥个图案中的棋子数量。
将n=6代入公式，得到$\frac{6 × (6 + 1)}{2} = \frac{6 × 7}{2} = 21$。
【答案】：
B. 21。

3. 有一种密码,将英文26个字母a,b,c,…,z(不论大小写)依次对应1,2,3,…,26,这26个自然数(见表),当明文对应的序号x为奇数时,密文对应的序号为$\frac{|x-25|}{2}$,当明文对应的序号x为偶数时,密文对应的序号为$\frac{x}{2}+3$. 按上述规定,将明文“agfo”译成密文是( B ).
A.like
B.life
C.look
D.love

答案： 【解析】：
本题主要考查了密码的对应转换。
首先，我们需要知道每个字母对应的数字，
a 对应 1，
g 对应 7，
f 对应 6，
o 对应 15。
接下来，根据题目给出的规则进行转换：
当明文对应的序号 x 为奇数时，密文对应的序号为 $\frac{|x-25|}{2}$，
当明文对应的序号 x 为偶数时，密文对应的序号为 $\frac{x}{2}+3$，
对于 a（序号 1，奇数）：
密文序号 =$\frac{|1-25|}{2}=\frac{24}{2}=12$，
12 对应的字母是 l。
对于 g（序号 7，奇数）：
密文序号 = $\frac{|7-25|}{2}=\frac{18}{2}=9$，
9 对应的字母是 i。
对于 f（序号 6，偶数）：
密文序号 = $\frac{6}{2}+3=3+3=6$，
6 对应的字母是 f。
但是我们需要的是密文的字母，根据密文序号找到对应的密文字母，
f 加密后对应的是 $\frac{6}{2}+3=6$，6 对应字母表中的 f 往后移动三位是 i（因为加密是+3），这里是直接对应，所以就是 i 的下一个计算需要加 3 后的结果找对应字母，
而实际上我们直接按公式算出的就是密文序号，
所以直接取公式结果对应的字母即可，即：
密文序号 6 对应的是字母表中的第 6 个字母，即 f（但按加密规则我们直接取公式结果对应的，这里解释是为了理解过程，实际操作中直接对应即可），
而按加密公式，偶数序号直接算出的结果就是密文序号，对应字母即可，
所以这里是 i（因为我们是直接用公式算出序号后，找对应字母，不是真的去字母表中往后移动）。
对于 o（序号 15，奇数）：
密文序号 = $\frac{|15-25|}{2}=\frac{10}{2}=5$，
5 对应的字母是 e。
所以，明文“agfo”对应的密文是“life”。
【答案】：B

4. 如图,四位同学站成一排,按图中所示规律数数,数到2025对应的同学是小平.

答案： 解：观察规律，数数顺序为1→2→3→4→5→6→7→8→9→10→11→12→13→14→15→16→17…，每6个数为一个循环周期，对应同学顺序为：小吉、小祥、小平、小安、小平、小祥。
2025÷6=337……3，余数为3。
循环周期中第3个对应小平。
答案：小平

5. 观察下列各式：
1×5+4= $3^2$,①
3×7+4= $5^2$,②
5×9+4= $7^2$,③
…
探索以上式子的规律,试写出第n个等式：$(2n-1)(2n+3)+4=(2n+1)^2$.

答案： 【解析】：
观察给出的等式，我们可以发现每个等式的左侧是两个奇数的乘积加4，而右侧则是一个奇数的平方。
1. 对于第一个等式 $1×5+4=3^2$，可以观察到 $1=2×1-1$，$5=2×1+3$，$3=2×1+1$。
2. 对于第二个等式 $3×7+4=5^2$，可以观察到 $3=2×2-1$，$7=2×2+3$，$5=2×2+1$。
3. 对于第三个等式 $5×9+4=7^2$，可以观察到 $5=2×3-1$，$9=2×3+3$，$7=2×3+1$。
根据以上观察，我们可以发现每个等式的左侧的两个奇数可以表示为 $2n-1$ 和 $2n+3$，其中 $n$ 是等式的序号（从1开始）。而等式右侧的平方数则是 $2n+1$ 的平方。
因此，第 $n$ 个等式可以表示为：$(2n-1)(2n+3)+4=(2n+1)^2$。
【答案】：
$(2n-1)(2n+3)+4=(2n+1)^2$

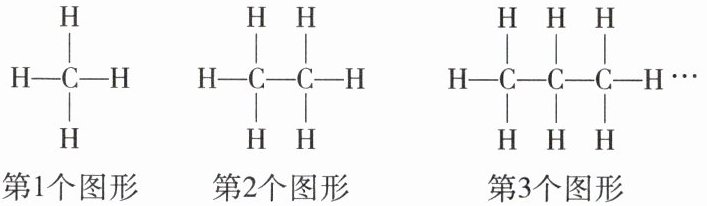
6. (2023东莞期末)将字母“C”“H”按照如图所示的规律摆放,依次下去,则第n(n为正整数)个图形中字母“H”的个数为______(用含n的代数式表示).

2n + 2

答案： 【解析】：
本题可先分别找出前几个图形中字母“H”的个数，再分析其规律，进而得出第$n$个图形中字母“H”的个数。
步骤一：分析前几个图形中字母“H”的个数
第$1$个图形中字母“H”的个数为$4$。
第$2$个图形中字母“H”的个数为$6$。
第$3$个图形中字母“H”的个数为$8$。
步骤二：寻找规律
观察上述数据，发现相邻两个图形中字母“H”的个数相差$2$，即后一个图形比前一个图形多$2$个字母“H”。
由此可推测，第$n$个图形中字母“H”的个数是一个首项$a_1 = 4$，公差$d = 2$的等差数列的第$n$项。
根据等差数列的通项公式$a_n=a_1+(n - 1)d$（其中$a_n$为第$n$项的数值，$a_1$为首项，$n$为项数，$d$为公差），可得第$n$个图形中字母“H”的个数为：
$4 + (n - 1)×2$
步骤三：化简代数式
对$4 + (n - 1)×2$进行化简：
$\begin{aligned}4 + (n - 1)×2&=4 + 2n - 2\\&=2n + 2\end{aligned}$
【答案】：$2n + 2$

7. 观察一组式子：2x,$-4x^2$,$6x^3$,$-8x^4$,…,$38x^{19}$,$-40x^{20}$,…,回答下列问题：
(1)请分别写出第5个、第6个式子.
(2)根据上面的归纳,你可以猜想出,第n个式子是什么？
(3)请你根据猜想,分别写出第2025个、第2026个式子.

答案： 【解析】：
(1)观察给出的数列：2x, $-4x^2$, $6x^3$, $-8x^4$, …, 可以看出每个式子的系数是递增的偶数，且符号交替出现。第5个式子的系数应为10（因为$2+4+2+2=10$，且为正数因为它是奇数位置），次数为5，所以第5个式子为$10x^5$。同理，第6个式子的系数应为-12（因为$10+2=12$，且为负数因为它是偶数位置），次数为6，所以第6个式子为$-12x^6$。
(2)对于第n个式子，其系数的绝对值是2n，且当n为奇数时系数为正，当n为偶数时系数为负。这可以通过$(-1)^{n+1}$来调节系数的正负。因此，第n个式子可以表示为$(-1)^{n+1} × 2n × x^n$。
(3)根据
(2)中的猜想，第2025个式子的系数应为$(-1)^{2025+1} × 2 × 2025 = 4050$（正数，因为2025是奇数），次数为2025，所以第2025个式子为$4050x^{2025}$。同理，第2026个式子的系数应为$(-1)^{2026+1} × 2 × 2026 = -4052$（负数，因为2026是偶数），次数为2026，所以第2026个式子为$-4052x^{2026}$。
【答案】：
(1)第5个式子为$10x^5$，第6个式子为$-12x^6$。
(2)第n个式子为$(-1)^{n+1} × 2n × x^n$。
(3)第2025个式子为$4050x^{2025}$，第2026个式子为$-4052x^{2026}$。