《2025年云南省标准教辅优佳学案七年级数学上册人教版》

5.已知A,B两地相距720 km,一列快车从A地开出,每小时行100 km；一列慢车从B地开出,每小时行80 km.
(1)两车同时开出,相向而行,x h相遇,则可列方程为$100x + 80x = 720$；
(2)两车同时开出,同向而行,x h后快车追上慢车,则可列方程为$100x - 80x = 720$；
(3)两车同时开出,背向而行,x h后两车相距1080 km,则可列方程为$720 + 100x + 80x = 1080$；
(4)慢车先开出1 h,两车相向而行,慢车开出多少小时后两车相距280 km?
解：设慢车开出$y$小时后两车相距$280$km。
情况一：相遇前相距$280$km
$80y + 100(y - 1) + 280 = 720$
$80y + 100y - 100 + 280 = 720$
$180y + 180 = 720$
$180y = 540$
$y = 3$
情况二：相遇后相距$280$km
$80y + 100(y - 1) - 280 = 720$
$80y + 100y - 100 - 280 = 720$
$180y - 380 = 720$
$180y = 1100$
$y = \frac{55}{9}$
答：慢车开出$3$小时或$\frac{55}{9}$小时后两车相距$280$km。

答案： 解：设慢车开出$y$小时后两车相距$280$km。
情况一：相遇前相距$280$km
$80y + 100(y - 1) + 280 = 720$
$80y + 100y - 100 + 280 = 720$
$180y + 180 = 720$
$180y = 540$
$y = 3$
情况二：相遇后相距$280$km
$80y + 100(y - 1) - 280 = 720$
$80y + 100y - 100 - 280 = 720$
$180y - 380 = 720$
$180y = 1100$
$y = \frac{55}{9}$
答：慢车开出$3$小时或$\frac{55}{9}$小时后两车相距$280$km。

6.某商场在“十一”国庆节假期期间投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如下表：

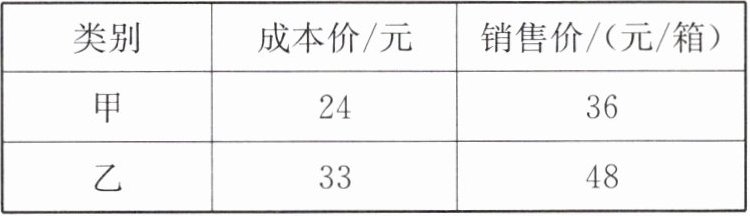
(1)该商场购进甲、乙两种矿泉水各多少箱？
(2)为了促销,该商场将甲种矿泉水打九折出售,将乙种矿泉水打八五折出售,这样500箱矿泉水在“十一”国庆节假期结束时全部售完.该商场可获得利润多少元？

答案：
(1)设购进甲种矿泉水$x$箱，则购进乙种矿泉水$(500 - x)$箱。
根据题意，得$24x + 33(500 - x)=13800$
解得$x = 300$
$500 - x=500 - 300 = 200$
答：购进甲种矿泉水300箱，乙种矿泉水200箱。
(2)甲种矿泉水利润：$300×(36×0.9 - 24)=300×(32.4 - 24)=300×8.4 = 2520$（元）
乙种矿泉水利润：$200×(48×0.85 - 33)=200×(40.8 - 33)=200×7.8 = 1560$（元）
总利润：$2520 + 1560 = 4080$（元）
答：该商场可获得利润4080元。

7.某玩具工厂出售一种玩具,其成本价为每件28元.如果直接由厂家门市部销售,每件产品售价为35元,同时每月还要支出其他费用2100元；如果委托商场销售,那么出厂价为32元.
(1)在两种销售方式下,每个月销售多少件时,所得利润相等？
(2)若每个月销售量达到1000件,则采用哪种销售方式获得的利润较多？

答案： 【解析】：
本题主要考查一元一次方程的应用，特别是在实际商业环境中，如何根据售价、成本和额外费用来计算利润，并找出两种销售方式下利润相等的销售量。
首先，我们需要分别建立两种销售方式的利润公式。对于厂家门市部销售，每件利润是$35-28=7$元，但每月还有额外费用$2100$元，所以总利润是$7x - 2100$元（$x$是销售量）。对于委托商场销售，每件利润是$32-28=4$元，没有额外费用，所以总利润是$4x$元。
(1) 为了找出两种销售方式利润相等的销售量，我们可以设置等式$7x - 2100 = 4x$，然后解这个方程来找出$x$的值。
(2) 为了比较在销售量达到$1000$件时哪种销售方式利润更多，我们可以将$x=1000$分别代入两个利润公式中进行计算。
【答案】：
(1) 解：
设每月销售$x$件时，两种销售方式所得利润相等，
根据题意，我们可以列出方程：
$7x - 2100 = 4x$
移项得：
$3x = 2100$
解得：
$x = 700$
答：每月销售$700$件时，两种销售方式所得利润相等。
(2) 当每月销售达到$1000$件时，
厂家门市部销售的利润为：
$7 × 1000 - 2100 = 4900 (元]$
委托商场销售的利润为：
$4 × 1000 = 4000 (元]$
因为$4900 ＞ 4000$，
所以采用厂家门市部销售方式获得的利润较多。
答：若每个月销售量达到$1000$件时，采用厂家门市部销售方式获得的利润较多。